This section covers:

paloittelufunktiot (tai paloittelufunktiot) ovat juuri sitä, mitä ne on nimetty: eri funktioiden palaset (alifunktiot) kaikki yhdellä graafilla. Helpoin tapa ajatella niitä on, jos piirsit enemmän kuin yhden funktion kuvaajaan, ja poistit vain osia funktioista, joissa niiden ei pitäisi olla (\(x\): n varrella); ne on määritelty eri tavalla eri intervalleille \(x\). \(y\) on määritelty eri tavalla \(x\): n eri arvoille; käytämme \(x\): tä etsimään, missä välissä se on, jotta voimme selvittää, mitä \(y\): n pitäisi olla.
huomaa, että on olemassa esimerkki paloittain funktion käänteisestä tässä funktioiden Käänteisosassa.
Here’s an example and graph:
|
Piecewise Function |
Graph |
|
\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ if }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ if }x>-2\end{align} \right.\) (on muitakin tapoja näyttää tämä, kuten käyttämällä ”for” sijasta ”jos”, ja käyttämällä pilkkuja tai puolipisteitä sijasta ”jos”.) Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\mathbb{R},\,\,\text{or}\,\,\left ({- \infty, \infty} \right)\) |
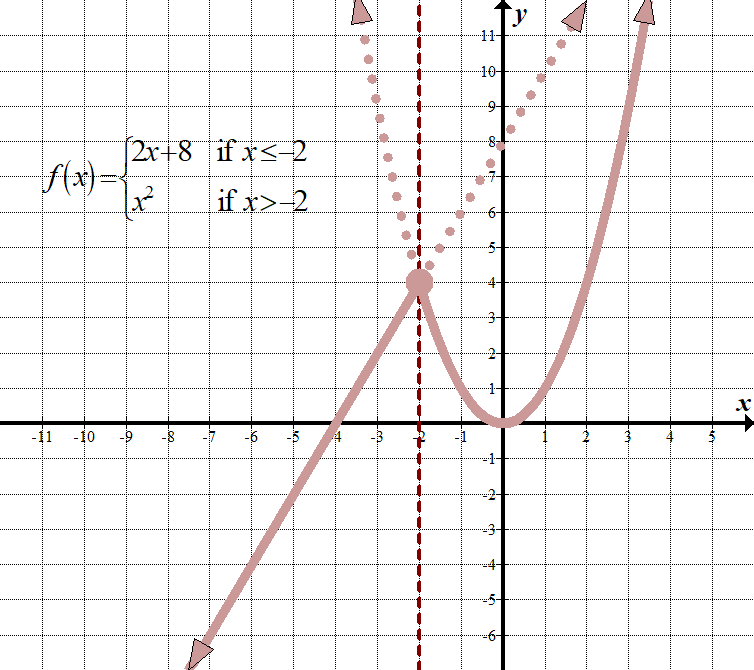 |
mitä tämä tarkoittaa on jokaiselle\(x\) pienempi tai yhtä suuri kuin -2, meidän täytyy piirtää viiva\ (2x+8\), ikään kuin se olisi ainoa funktio kuvaajassa. Jokaiselle \(x\) arvolle, joka on suurempi kuin -2, meidän täytyy piirtää \({{x}^{2}}\), ikään kuin se olisi ainoa funktio kuvaajassa. Sitten meidän on ”hankkiuduttava eroon” niistä osista, joita emme tarvitse. Muista, että käytämme edelleen Originia vertailukohtana molemmille kuvaajille!
Katso miten pystyviiva \(x=-2\) toimii ”rajana” kahden kuvaajan välillä?
huomaa, että pisteellä \((-2,4)\) on siinä suljettu ympyrä. Teknisesti sen pitäisi kuulua vain \(2x+8\) funktioon, koska funktiolla on pienempi tai yhtä suuri merkki, mutta koska piste on myös \({{x}^{2}}\) kaaviossa, Voimme käyttää suljettua ympyrää ikään kuin se esiintyisi molemmissa funktioissa. Ei hassumpaa, vai mitä?
Evaluating Piecewise Functions
Sometimes, you ’ ll be given piecewise functions and asked to evaluate them; toisin sanoen, etsi \(y\) arvot, kun sinulle annetaan \(x\) arvo. Tehdään tämä \(x=-6\) ja \(x=4\) (Ilman kaaviota). Tässä on taas funktio:
\(\displaystyle f\left (x \right) = \left\{ \begin{align}2x+8\,\,\,\,\,& \text{ if }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text { }\, &\text{ if }x>-2\end{align} \right.\)
haluamme ensin katsoa, missä meidän \(x\) on. Kun \(x=-6\), tiedämme, että se on alle -2, joten liitämme \(x\) \(2x+8\) vain. \(f (x)\) tai \(y\) on \((2)(-6)+8=-4\). Emme edes välitä \(\boldsymbol{{x}^{2}}\)! Se on niin helppoa. Voit myös nähdä, että teimme tämän oikein käyttämällä yllä olevaa graafia.
kokeile nyt \(x=4\). Katsomme ensin oikeaa ja näemme, että \(x\) on suurempi kuin -2, joten liitämme sen \({{x}^{2}}\). (Voimme vain sivuuttaa \(2x + 8\) tällä kertaa.) \(f (x)\) tai \(y\) on \({{4}^{2}}=16\).
piirtävät paloittain funktioita
sinua luultavasti pyydetään piirtämään paloittain funktioita. Joskus kuvaajat sisältävät funktioita, jotka eivät ole jatkuvia tai epäjatkuvia, mikä tarkoittaa, että sinun täytyy poimia kynäsi keskelle kuvaajaa, kun piirrät sitä (kuten hyppy!). Jatkuvat funktiot tarkoittavat sitä, että sinun ei koskaan tarvitse poimia kynääsi, jos haluat piirtää ne vasemmalta oikealle.
ja muista, että graafit ovat todellisia funktioita vain, jos ne läpäisevät Pystyviivatestin.
piirretään nämä paloittain tehtävät ja määritetään, ovatko ne jatkuvia vai ei-jatkuvia. Huomaa, miten piirrämme jokaisen funktion ikään kuin se olisi ainoa, ja sitten ”poistaa” osat, joita ei tarvita. Saamme myös verkkotunnuksen ja alueen, kuten teimme täällä algebrallisten funktioiden osiossa.
| Piecewise Function | Graph |
|
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\left( {0,\infty } \right)\) |
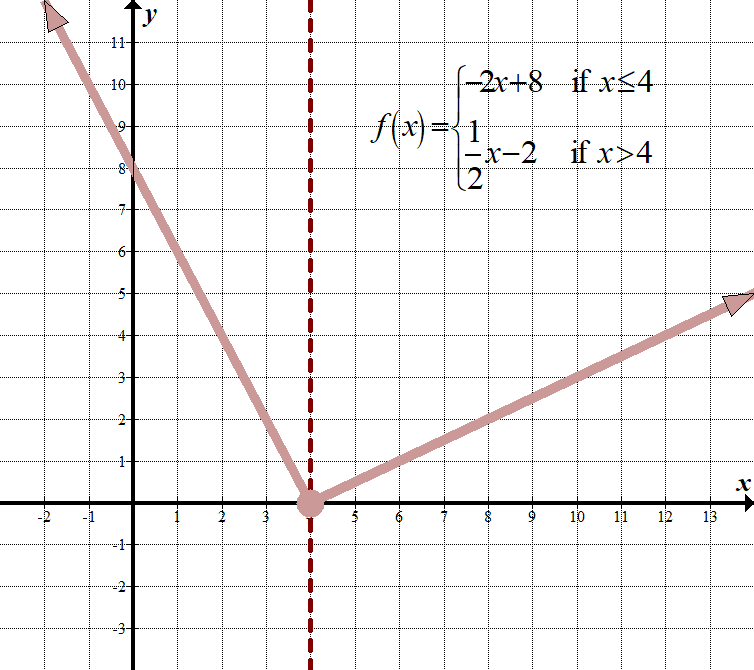 |
|
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1}\le x<4\\x-5\,\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\) Non-Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) |
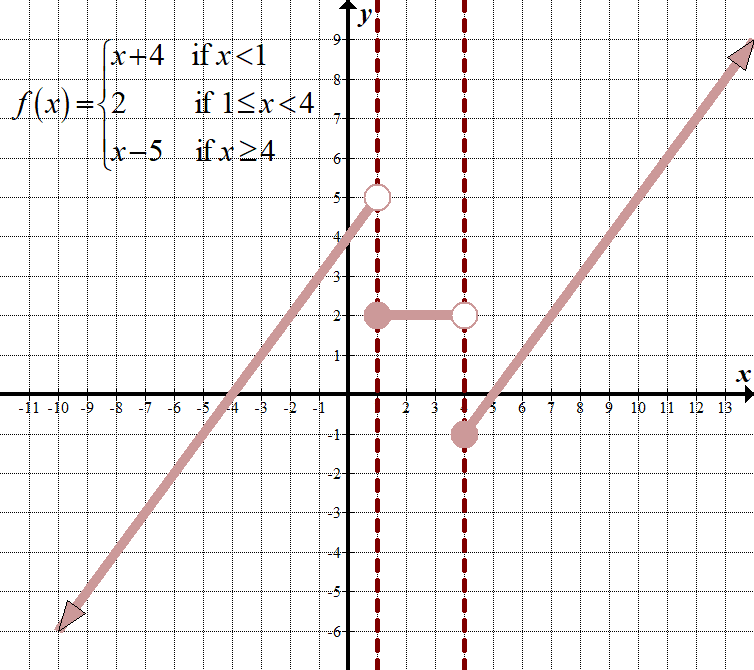 |
We can actually put piecewise functions in the graphing calculator:
| Piecewise Function Screens | Steps and Notes |
| Enter the piecewise function on three lines:
tässä on kaavio:
|
laittaa paloittain funktion \(\displaystyle f\left( x \right)=\left\ {\\begin{array}{L}x+4\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le x<4\\-5 + x\,\,\,\,\,\teksti{if }x\ge 4\end{array} \right.\ ) laskimessa voit syöttää funktion kolmelle riville jakamalla funktion kussakin intervallissa kyseisen intervallin ”testiepäyhtälöllä” (ja katso sulkeet!).
syy, miksi jaamme intervalleilla tai epäyhtälöillä on se, että laskija palauttaa arvon 1, jos epäyhtälö (kuten \(x<1\) on tosi; esimerkiksi \((x+4)\) vain päätyy \((x+4)/(1)\), Kun \(x<1\). Kun \(x\ge 1\), jaamme 0: lla, joten mitään ei piirretä. Tässä on mitä voimme laittaa laskin: \(\displaystyle \begin{array}{l}{{Y}_{1}}=\left( {x+4} \right)/\left( {x<1} \right)\\{{Y}_{2}}=\left( 2 \right)/\left( {x\ge 1\text{ ja }X<4} \right)\\{{y}_{3}}=\left( {-5+x} \right)/\left( {x\ge 4} \right)\end{array}\) (huomaa, että voit kirjoittaa tämän myös yhdellä rivillä kertomalla ehdot jakamisen sijaan ja käyttämällä plus-merkkejä jokaisen kolmen funktion/intervallin välillä: \(\displaystyle {{Y}_{1}}=\left( {x+4} \right)\left( {x<1} \right)+\left ({x \right)\left ({x\ge 1\text {and }x<4} \right)+\left ({-5+x} \right)\left ({x\\ge 4}\right)\).) tässä on näppäilyt kolmen rivin käyttöön. Huomaa, että käytät 2nd MATH (testi) päästä näytön, joka on \(\le\), \(\ge\), ja niin edelleen. Esimerkiksi 2. Matematiikka 6 saa sinut \(\le \). Käytä 2. matematiikkaa (testi), oikeus logiikkaan, sitten 1, Kun ”ja” ovat \({{Y}_{2}}\).
|
Kuinka kertoa, onko paloittain funktio jatkuva vai ei-jatkuva
kertoa, onko paloittain kuvaaja jatkuva vai ei-jatkuva, sinä voi tarkastella rajapisteitä ja nähdä, onko \(y\) piste sama jokaisessa niistä. (Jos \(y\) n olivat erilaisia, siellä olisi ”hypätä” kaaviossa!)
kokeillaan tätä yllä käyttämillemme funktioille:
| Piecewise Function | Check Boundary Points |
| \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) | Let’s check \(x=4\) in both parts of the function, since 4 is the ”boundary point”:
\(\begin{array}{l}-2(4)+8=0\\\,\,\,\frac{1}{2}(4)-2=0\end{array}\) koska \(0=0\), tämä paloittain tehtävä on jatkuva. |
| \(\displaystyle F\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le x<4\\-5 + x\,\,\,\,\,\,\,\,\,\teksti{if }x\ge 4\end{array} \right.\) | tarkistetaan funktion kaksi ensimmäistä osaa. Huomaa toisessa osassa, \(y\) on aina 2:
\(\begin{array}{l}1+4=5\\\,\,\,\,\,\,\,\,\,2=2\end{array}\) koska \(5\ne 2\), voimme lopettaa tähän, ja huomaa, että tämä paloittain funktio on ei-jatkuva. Jos \ (y\): t olisivat yhtä suuret, olisi mentävä yksi tarkistaaksemme seuraavan rajapisteen kohdassa\(x=4\). |
yhtälöiden saamiseksi paloittain kuvaavista funktioista
sinua voidaan pyytää kirjoittamaan paloittain funktio kaavion mukaisesti. Nyt kun tiedämme, mitä paloittain toiminnot ovat kyse, se ei ole niin huono!
tarkastellaksesi, miten saadaan yhtälöt lineaarisista kaavioista, katso rivien yhtälöiden saaminen ja kvadratiikasta, katso Neliöyhtälön löytäminen pisteistä tai kuvaajasta.
tässä ovat kaaviot, joissa on selityksiä siitä, miten niiden paloittain yhtälöt saadaan:
| Piecewise Function Graph | Procedure to get Function |
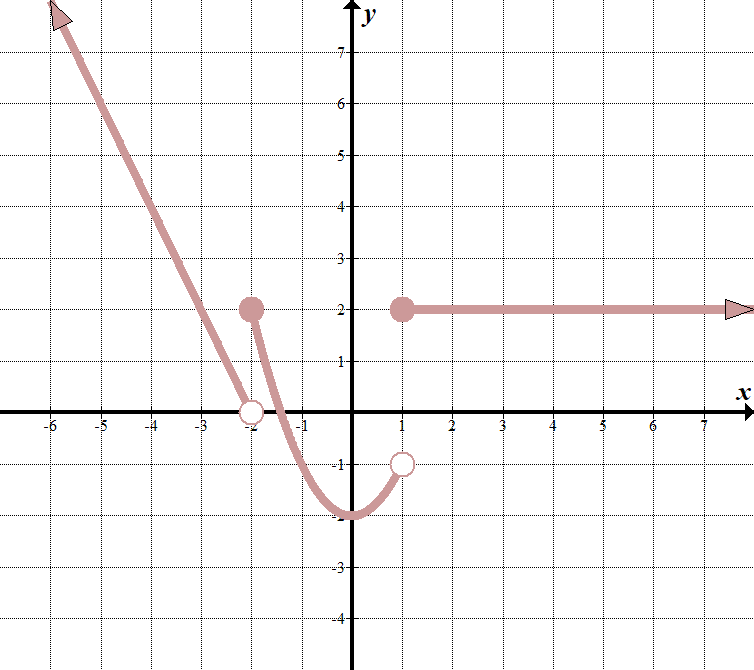 |
We see that our ”boundary lines” are at \(x=-2\) and \(x=1\). We know that our function will look something like this (notice open and closed endpoints):
\(\displaystyle F\left( x \right)=\left\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\text{if }x<-2\\ \ text{ }……\,\,\,\,\,\,\,\,\text{if }-\text{2 }\le x<1\\\text{ }……\,\,\,\,\,\,\,\,\Teksti{jos }x\ge 1\end{array} \right.\) voimme valita kaksi pistettä \((-2,0)\) ja \((-3,2)\) vasemmalta suoralta saadaksemme yhtälön \(y=-2x-4\). keskimmäinen funktio on \(y = {{x}^{2}}-2\), ja oikeanpuoleisin funktio on vain vaakasuora viiva \(y=2\). näin paloittain funktio on: \(\displaystyle F\left (x \right) = \left\{ \begin{array}{l}-2x-4\,\,\,\,\,\,\,\text{if }x<-2\\ \ text{ }{{x}^{2}}-2\,\,\,\,\,\,\,\,\,\,\text{if }-\text{2}\le x<1\\\text{ 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Teksti{jos }x\ge 1\end{array} \right.\) |
 |
näemme, että ”rajaviivamme” on \(x=5\). Koska rivit kohtaavat \((5,4)\), sillä ei ole väliä, mihin laitamme \(\le \) tai \(\ge\) – merkin; emme voi laittaa sitä molempiin paikkoihin, muuten se ei olisi funktio. Tähän mennessä:
\(\displaystyle F\left (x \right) = \left\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\,\text{if }x<5\\ \ text{ }……\,\,\,\,\,\,\,\,\,\Teksti{if }x\ge 5\end{array} \right.\) taas joudumme tarkastelemaan jokaista riviä erikseen määrittääksemme niiden yhtälöt. Voimme joko ottaa 2 pistettä jokaiselta riviltä saadaksemme nämä, tai johtaa rinteistä ja \(y\) – sieppauksista; paloittain funktio on: \(\displaystyle F\left( x \right)=\left\{ \begin{array}{l}\frac{6}{5}x-2\,\,\,\,\,\,\,\text{if }x<5\\\frac{2}{5}x+2\,\,\,\,\,\,\,\teksti{if }x\ge 5\end{array} \right.\) |
itseisarvo paloittain funktiona
voimme kirjoittaa itseisarvofunktioita paloittain – se on todella siistiä! Haluat ehkä tarkistaa solving itseisarvo yhtälöt ja eriarvoisuutta ennen kuin jatkat tähän aiheeseen.
sanotaan, että meillä on funktio \(f\left( x \right)=\left|x \right/\). Siitä, mitä opimme aiemmin, tiedämme, että kun \(x\) on positiivinen, koska otamme itseisarvon, se on silti vain \(x\). Mutta kun \(x\) on negatiivinen, kun otamme itseisarvon, meidän on otettava vastakohta (kumottava se), koska itseisarvon on oltava positiivinen. Käykö järkeen? Joten, esimerkiksi, jos meillä oli \(/5/\), otamme vain mitä on sisällä absoluuttinen merkki, koska se on positiivinen. Mutta \(/-5/\), meidän on otettava päinvastainen (negatiivinen) mitä sisällä itseisarvo tehdä \(\displaystyle 5\,\,\,(-\,-5=5)\).
tämä tarkoittaa, että voimme kirjoittaa tämän itseisarvofunktion paloittain. Huomaa, että voimme saada ”käännepisteen” tai ”rajapisteen” asettamalla sen, mikä on itseisarvon sisällä, arvoon 0. Sitten käytämme joko alkuperäistä funktiota tai nollaamme funktion, riippuen funktion merkistä (ilman itseisarvoa) kyseisellä aikavälillä.
esimerkiksi voidaan kirjoittaa \(\displaystyle \left / x \right / \text { } = \left\{ \begin{array}{l}x\,\,\,\,\,\,\,\,\,\teksti{if }x\ge 0\\ – x\,\,\,\,\,\text{if }x<0\end{array} \right.\). Huomaa myös, että jos funktio on jatkuva (ei ole” hypätä”) rajakohdassa, sillä ei ole väliä, missä laitamme” pienempi tai yhtä suuri ”(tai” suurempi tai yhtä suuri kuin”) merkkejä, kunhan emme toista niitä! Emme voi toistaa niitä, koska teoriassa meillä ei voi olla kahta arvoa \(y\) samalle \(x\), tai meillä ei olisi funktiota.
Here are more examples, with explanations. (You might want to review Quadratic Inequalities for the second example below):
| Absolute Value Function | Method to get Piecewise Function |
| \(g\left( x \right)=\left| {2x+3} \right|\) | Let’s first find the ”boundary line”. Teemme tämän asettamalla, mitä on sisällä itseisarvo 0, ja sitten ratkaista \(\boldsymbol{x}\).
kun \(2x+3\ge 0\), saamme \(\displaystyle x\ge -\frac{3}{2}\) (Itse asiassa voimme pitää \(\ge\), kun ratkaisemme). Kun \(2x + 3\) on positiivinen, otamme sen vain ”sellaisenaan”, mutta jos se on negatiivinen, meidän on kumottava koko asia. näin ollen paloittain funktio on: \(\displaystyle \left|{2x+3} \right / =\left\{ \begin{array}{l}2x+3\,\,\,\,\,\,\,\,\,\text{if }x\ge – \frac{3}{2}\text{ }\\-2x-3\,\,\,\,\,\text{if }x<-\frac{3}{2}\end{array} \right.\) kokeile – se toimii! |
| \(F\left( x \right)=\left|{{{x}^{2}}-4} \right/\) | etsitään ensin ”rajaviiva(s)”; asetetaan itseisarvon sisällä oleva arvo arvoon 0.
Kun \({{x}^{2}}-4\ge 0\), saadaan \(x\le -2\) tai \(x\ge 2\) (kokeile numeroita!). Kun \({{x}^{2}}-4\) on positiivinen, otamme sen vain ”sellaisena kuin se on”, mutta jos se on negatiivinen, meidän on kumottava se. paloittain funktio on: \(\displaystyle \left| {{{x}^{2}}-4} \right|=\left\{ \begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\text{if }x\le -2\\4 – {{x}^{2}}\,\,\,\,\,\text{if }-2< x<2\\{{x}^{2}}-4\,\,\,\,\,\text{if }x\ge 2\text{ }\end{array} \right.\ ) tai \(\displaystyle \left / {{{x}^{2}}-4} \right / = \left\{ \begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\text{if }x\le -2\text { }\,\, \text{tai}\,\,\text{ }x\ge 2\\4 – {{x}^{2}}\,\,\,\,\,\,\,\text{if }-2<x<2\end{array} \right.\) taas (koska funktio on jatkuva), ei oikeastaan ole väliä missä ovat \(\le\) ja \(\ge\) (vastakohtana \(<\) ja \(>\)), kunhan emme toista niitä. |
| \(F\left( x \right)=2x+\left|{x+2} \right/\) | tämä on hieman hankalampi, sillä meillä on \(x\) itseisarvon sisä-ja ulkopuolella. ”Rajaviivalle” käytämme vain sitä, mikä on itseisarvon sisällä.
kun \(x+2\ge 0\), saadaan \(x\ge -2\). Mutta paloittain tehtävää varten meidän on käytettävä koko funktiota, mukaan lukien osa, joka on itseisarvon ulkopuolella. Joten, paloittain funktio on: \(\displaystyle 2x+\left|{x+2} \right / =\left\{ \begin{array}{l}2x+x+2\,\,\,\,\,\teksti{if }x\ge -2\\2x-x-2\,\,\,\,\,\text{if }x<-2\end{array} \right.\) yksinkertaistetaan: \(\displaystyle 2x+\left| {x+2} \right|=\left\{ \begin{array}{l}3x+2\,\,\,\,\,\,\,\teksti{if }x\ge -2\\x-2\,\,\,\,\,\,\,\,\,\,\text{if }x<-2\end{array} \right.\) kokeile joitakin arvoja alle ja suuri sitten -2; niiden pitäisi toimia! |
| \(g\left( x \right)=\left| {{{x}^{2}}-4x-5} \right|\) | tämä on parhaiten ratkaistu merkkikaaviolla, koska meillä on kvadraattinen ja meidän on tiedettävä, missä funktio on positiivinen ja negatiivinen.
kerro ensin itseisarvofunktion sisällä oleva neliö \(\left ({x-5} \right)\left ({x+1} \right)\). Sitten käyttää merkki kaavio nähdä, missä tekijät ovat positiivisia ja negatiivisia, ja muistaa, että jos tekijät ovat positiivisia, käytämme funktio ”sellaisena kuin on”, ja jos tekijät ovat negatiivisia, teemme tyhjäksi funktio: \(\displaystyle \left|{{{x}^{2}}-4x-5} \right / =\left\{ \begin{array}{l}{{x}^{2}} – 4x-5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\teksti{jos }x\le -1\,\,\,\,\teksti{tai}\,\,\,\, x\ge 5\\ – \left ({{{x}^{2}} – 4x-5} \right)\,\,\,\,\text{if }-1<x<5\text{ }\end{array} \right.\) |
| \(\displaystyle g\left( x \right)=\frac{{\left| {x+2} \right|}}{{x+2}}\) | tämä on rationaalifunktio, koska nimittäjässä on muuttuja.
kun \(x+2\ge 0\), saadaan \(\displaystyle x\ge -2\). Kun \(x + 2\) on positiivinen, otamme sen ”sellaisena kuin se on”, mutta jos se on negatiivinen, meidän on mitätöitävä itseisarvo: \(\displaystyle \frac{{\left| {x+2} \right|}}{{x+2}}=\left\{ \begin{array}{l}\frac{{x+2}} {x+2}}\,\,\,\,\,\,\,\,\,\teksti{if }x\ge -2\\\frac {{- x-2}}{{x+2}}\,\,\,\,\,\,\text{if }x<-2\end{array} \right.\). Mutta meidän on oltava varovaisia, koska \(x\ne 2\) (toimialueen rajoitus: nimittäjä olisi 0). näin ollen paloittain funktio on: \(\displaystyle \frac {{\left| {x + 2} \right/}} {{x + 2}}=\left\{ \begin{array}{l}1\,\,\,\,\,\,\,\,\,\,\text{if }x>-2\\-1\,\,\,\,\,\,\text{if }x<-2\end{array} \right.\). |
sinua voidaan myös pyytää ottamaan itseisarvokäyrä ja kirjoittamaan se paloittain funktiona:
| Absolute Value Graph | Method to get Piecewise Function |
 |
We see that our ”boundary line” is at \(x=0\), so what’s inside the absolute value sign must be \(x\) or a factor of \(x\). (Tämä johtuu siitä, että saadaksemme rajaviivan itseisarvofunktiolla, asetamme sen, mikä on itseisarvon sisällä, arvoon 0, ja ratkaisemme \(x\)).
kun \(x>0\), voidaan nähdä, että janan yhtälö on \(y=2x-2\). Kun \(x<0\), yhtälö on \(y=2x-2\). Voimme kirjoittaa tämän paloittain funktiona: \(\displaystyle f\left (x \right) = \left\{ \begin{array}{l}2x-2\,\,\,\,\,\,\,\text{if }x>0\\-2x-2\,\,\,\text{if }x\le 0\end{array} \right.\) voimme kirjoittaa tämän myös muunnettuna itseisarvofunktiona: \(y=2\left / x \right| -2\) tai \(y=\left|{2x} \right| -2\) (koska 2 on positiivinen, se voi olla \(\left|{ \ ,\,} \right/\) sisä-tai ulkopuolella). (Tässä on järkeä, sillä kun \(\left| { \ ,\,} \right|\) on \(> 0\), käytämme säännöllistä funktiota \(y=2x-2\), ja kun sen sisällä oleva on \(< 0\), poistamme itseisarvon osan tehdäksemme siitä \(y=-\left( {2x} \right)-2\)). |
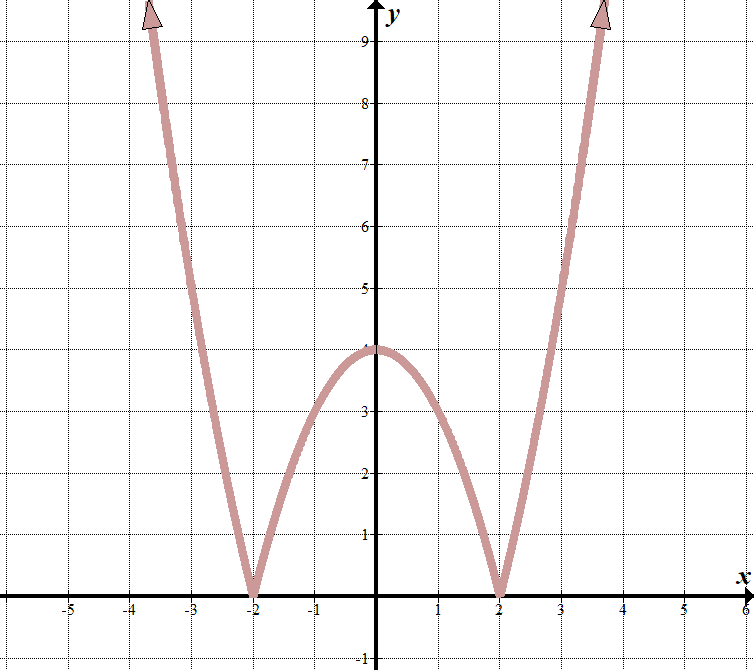 |
näemme, että ”rajaviivamme” ovat \(x=2\) ja \(x=-2\), joten sillä, mikä on itseisarvomerkin sisällä, täytyy olla tekijöitä \(x-2\) ja \(x+2\).
kun \(x<-2\) tai \(x>2\), voidaan nähdä, että kuvaaja näyttää graafin normaalilta osalta \(y={x}^{2}}-4\). (Olen tajunnut tämän tietämällä tekijät, ja ottaen hyvä arvaus!) Kun \(-2<x<2\), yhtälö käännetään eli nollataan (käännetään \(x\)-akselin yli). Voimme kirjoittaa tämän paloittain funktiona: \(\displaystyle f\left (x \right) = \left\{ \begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\,\,\,\text{if }x<-2\text{ or }x>2\\ – {{x}^{2}}\text{+ 4}\,\,\,\,\,\,\teksti{if }-2\le x\le 2\end{array} \right.\) voidaan nähdä, että tästä alkoi muunnettu kvadraattinen funktio \(y={{x}^{2}}-4\), jonka ympärillä on itseisarvo, koska kaikki \(y\) arvot ovat positiivisia: \(y=\left| {{{x}^{2}}-4} \right|\). |
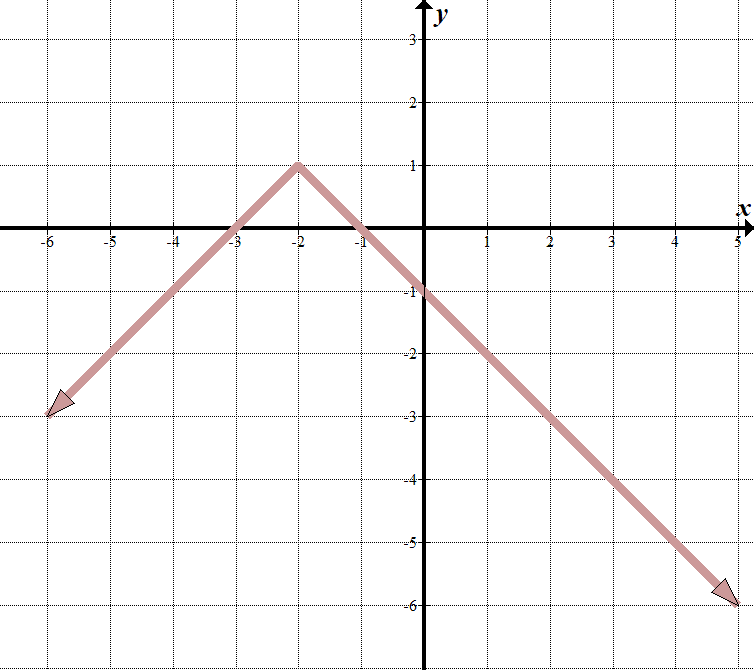 |
näemme, että ”rajaviivamme” on \(x=-2\), joten sen, mitä itseisarvomerkin sisällä on, on oltava \(x+2\).
kun \(x>-2\), voidaan nähdä, että janan yhtälö on \(y=-x-1\). Kun \(x<-2\), rivi on \(y=x+3\). Voimme kirjoittaa tämän paloittain funktiona: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-x-1\,\,\,\,\,\,\text{if }x>-2\\x+3\,\,\,\,\,\,\,\,\,\,\teksti{jos }x\le -2\end{array} \right.\) tätä lienee helpompi kirjoittaa muuntuneena itseisarvofunktiona. Voimme nähdä, että vanhemman itseisarvofunktio käännetään pystysuunnassa, siirretään vasemmalle 2 ja ylös 1. Itseisarvoyhtälömme on \(y= – \left / {x + 2} \right|\,\,+\,\,1\). Tämä on sama kuin paloittain funktio edellä. Kokeile – se toimii! |
Paloittelufunktioiden muunnokset
tehdään paloittelufunktion muunnos. Opimme miten vanhemman toiminnot ja niiden muunnokset täällä vanhemman kaaviot ja muunnokset osiossa. Haluat todennäköisesti lukea tämän osion ensin, ennen kuin yrität paloittain muutosta.
muutetaan seuraava paloittain \(x\)-akselin ympäri käännetty funktio pystysuunnassa venytettynä kertoimella 2 yksikköä, 1 yksikkö oikealle ja 3 yksikköä ylöspäin.
piirretään \(- 2F\left (x-1 \right)+3\), missä:
\(\displaystyle f\left( x \right)=\left\{ \begin{align}x+4\,\,\,\,\,\,\,\,& \text{ if }x<&\text{ if 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,&\text{ if }x\ge 4\end{align} \right.\)
Varmistakaamme, että käytämme” rajan ” pisteitä, kun täytämme t-kaavion muunnokselle. Muista, että muunnokset sisällä suluissa tehdään \(x\) (tekee päinvastainen matematiikka), ja ulkopuolella tehdään \(y\). Keksiä t-chart, kuten alla olevassa taulukossa, Voimme käyttää keskeisiä kohtia, mukaan lukien kaksi pistettä kunkin ”raja linjat”.
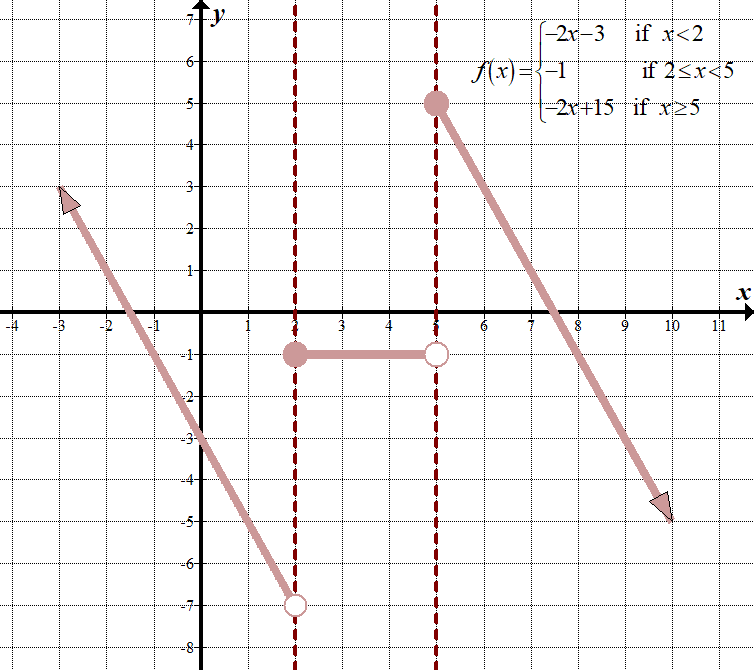
huomaa, että koska tämä muunnos on monimutkainen, voimme keksiä uuden paloittain tehtävän muuttamalla 3 ”kappaletta” ja myös muuttamalla ”\(x\)”s: t, joissa rajapisteet ovat (lisäämällä 1 tai menemällä oikealle 1), koska teemme päinvastaisen matematiikan ”\(x\)”s: ille. Saadaksemme uudet funktiot jokaiseen intervalliin, voimme vain korvata ”\(x-1\)” ja ”\(x\)” alkuperäisessä yhtälössä, kertoa -2: lla ja sitten lisätä 3. Esimerkiksi \(\displaystyle-2F\left( {x-1} \right)+3=-2\left+3=-2\left( {x+3} \right)+3=-2x-3\).
\(\displaystyle-2F\left( {x-1} \right)+3=\left\{ \begin{array}{L}-2\left( {\left( {x-1} \right)+4} \right)+3=-2x-3,\,\,\,\,\text{ if }x-1<1\,\,\,\left( {x<2} \right)\\-2\left( 2 \right)+3=-1,\,\,\,\,\text{ if }\,\text{ 2 }\le x<5\\-2\left( {\left( {x-1} \right)-5} \right)+3= – 2x+15,\,\,\,\,\teksti{ if }x\ge 5\end{array} \right.\)
tässä ovat” ennen ”- ja” jälkeen ” – kaaviot, mukaan lukien t-kaavio:
| Piecewise Parent Function | T-chart | Transformation of Function | ||||||||||||||||||||||||||||||||||||||||
| \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\)
|
|
\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2x-3\,\,\,\,\,\,\,\,\,\text{if }x<2\\-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 2}\le x<5\\-2x+15\,\,\,\,\,\,\text{if }x\ge 5\end{array} \right.\)
|
||||||||||||||||||||||||||||||||||||||||
Piecewise Function Word Problems
 Problem:
Problem:
suosikkikoirasi groomer veloittaa koirasi painon mukaan. Jos koira on 15 puntaa ja alle, groomer veloittaa $35. Jos koirasi on 15-40 puntaa, hän veloittaa 40 dollaria. Jos koirasi on yli 40 kiloa, hän veloittaa $40, plus ylimääräinen $2 jokaista kiloa.
(a) Kirjoita paloittain funktio, joka kuvaa mitä koirasi groomer lataa.
(b) kuvaa funktiota.
(c) mitä sulhaspoika laskuttaisi, jos Söpö koirasi painaa 60 kiloa?
ratkaisu:
(a) näemme, että ”rajapisteet” ovat 15 ja 40, koska nämä ovat painoja, joissa hinnat muuttuvat. Koska meillä on kaksi rajapistettä, meillä on kolme yhtälöä paloittain funktiossamme. Meidän täytyy aloittaa 0, koska koirien täytyy painaa yli 0 kiloa:
\(\displaystyle F\left( x \right)=\left\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\,\text{if }0<x\le 15\\ \ text{ }……\,\,\,\,\,\,\,\,\,\text{if }15<x\le 40\\ \ text{ }……\,\,\,\,\,\,\,\,\,\text{if }x>40\end{array} \right.\)
etsimme ”vastauksia ”(kuinka paljon trimmaus maksaa)” kysymyksiin ” (kuinka paljon koira painaa) kolmen hintaluokan osalta. Kaksi ensimmäistä ovat vain kiinteitä maksuja ($35 ja $40, vastaavasti). Viimeinen yhtälö on hieman hankalampi; groomer veloittaa $40 plus $2 jokaista puntaa yli 40. Kokeillaan todellisia numeroita: jos koirasi painaa 60 kiloa, hän veloittaa $40 plus $2 kertaa \(20(60-40)\). Teemme tästä yhtälön: \(40+2 (x–40)\), joka yksinkertaistaa \(2x–40\) (katso miten 2 on kaltevuus?).
koko paloiteltu funktio on:
\(\displaystyle F\left( x \right)=\left\{ \begin{array}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }0<x\le 15\\ \ text{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }15<x\le 40\\ \ text{ }40+2\left ({x-40} \ right)\,\,\,\,\,\,\text{if }x>40\end{array} \right.\ ) tai \(\displaystyle F\left (x \right) = \left\{ \begin{array}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }0<x\le 15\\ \ text{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }15< x\le 40\\ \ text{ }2x-40\,\,\,\,\,\,\,\text{if }x>40\end{array} \right.\)
(b) kuvaamme: huomaa, että tämä paloittain yhtälö on ei-jatkuva. Huomaa myös kohtuullinen verkkotunnus tämä ongelma voi olla \(\left ({0,200} \ right]\) (koska koirat eivät paina yli 200 kiloa!) ja kohtuullinen alue voi olla \(\left\cup \left\).
huomaa, että tämä paloittain yhtälö on ei-jatkuva. Huomaa myös kohtuullinen verkkotunnus tämä ongelma voi olla \(\left ({0,200} \ right]\) (koska koirat eivät paina yli 200 kiloa!) ja kohtuullinen alue voi olla \(\left\cup \left\).
(c) jos koirasi painaa 60 kiloa, voimme joko käyttää graafia tai funktiota nähdäksemme, että joudut maksamaan 80 dollaria. Vau! Se maksaa enemmän kuin ihmisen hiustenleikkuu (ainakin minun hiustenleikkuu)!
ongelma:
aiot myydä She Love Math-T-paitoja rahankeräyksenä. Tukkumyyjä veloittaa 10 dollaria paidalta 75 ensimmäisestä paidasta. Ensimmäisten 75 paidan jälkeen ostat jopa 150 paitaa, yhtiö laskee hintansa 7,50 dollariin per paita. Kun ostat 150 paitaa, hinta laskee 5 dollariin per paita. Kirjoita funktio, joka mallintaa tätä tilannetta.
ratkaisu:
näemme, että ”rajapisteet” ovat 75 ja 150, koska nämä ovat ostettujen t-paitojen määrä, jossa hinnat muuttuvat. Koska meillä on kaksi rajapistettä, meillä on kolme yhtälöä paloittain funktiossamme. Aloitamme \(x\ge 1\), koska oletamme ainakin yksi paita on ostettu. Huomaa tässä ongelma, määrä T-paitoja ostettu (\(x\)), tai verkkotunnus, on oltava kokonaisluku, mutta tämä rajoitus ei pitäisi vaikuttaa lopputulokseen ongelma.
\(\displaystyle F\left( x \right)=\left\{ \begin{array}{l}\text {}….. \text{ if }1\le x\le 75\\\text {}….. \text{ if }75<x\le 150\\\text {} \text {}……\text{if} X>150 \end {array} \ right.\)
etsimme ”vastauksia” (t-paitojen kokonaiskustannukset) ”kysymyksiin” (kuinka monta ostetaan) kolmen hintaluokan osalta.
enintään 75 paidan hinta on 10 dollaria, joten kokonaishinta olisi \(10x\). Yli 75 mutta jopa 100 paidan hinta on 7,50 dollaria, mutta ensimmäiset 75 t-paitaa maksavat silti 10 dollaria per paita. Toinen toiminto sisältää 750 dollaria käytetty ensimmäinen 75 paidat (75 kertaa $10), ja myös 7,50 dollaria kertaa enemmän paitoja yli 75, joka olisi \((x-75)\). Esimerkiksi, jos olet ostanut 80 paitoja, sinun täytyy viettää \(\$10 \ kertaa 75 = \$750\), plus \(\$7.50\kertaa 5\,\) (80 – 75) 75. paidan jälkeen.
vastaavasti yli 150 paidasta maksaisimme edelleen 10 dollarin hinnan 75 paidasta ylöspäin, 7 dollaria.50 hinta 76-150 paitaa (75 paitaa lisää), ja sitten 5 dollaria per paita yli 150 ostettujen paitojen määrästä. Me maksamme \(10(75)+7.50(75)+5(x-150)\) \(x\) – paidoille. Laita numerot ja kokeile!
koko paloiteltu funktio on:
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }1\le x\le 75\\ \ text{ }7.5 x\text { } + \text{ }187.5\,\,\,\,\,\text{if 7}5<x\le 150\\\text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\text{ if }x>150\end{array} \right.\ ) tai \(\displaystyle F\left (x \right) = \left\{ \begin{array}{l}\text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }1\le x\le 75\\ \ text{ }7.5 x\text { } + \text{ }187.5\,\,\,\,\,\text{if 7}5< x\le 150\\ \ text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\,\text{if }x>150\end{array} \right.\)
ongelma:
bussiyhteys maksaa 50 dollaria ensimmäiseltä 400 maililta, ja jokainen ylimääräinen 300 mailia (tai sen murto-osa) lisää 10 dollaria hintaan.
käytä paloittain funktiota, joka kuvaa bussin hintaa kilometrien etäisyytenä.
ratkaisu:
Tämä on itse asiassa hankala ongelma, mutta mietitään ensin ”rajapistettä”, joka on 400. Se on melko yksinkertaista, kun ratsastaa on alle 400 mailia; hinta on $50.
suuremmalla kuin 400 maililla meidän on vähennettävä ensimmäiset 400 mailia (mutta muista sisällyttää ensimmäinen 50 dollaria), jaettava jäljellä olevien mailien määrä 300 maililla (ja pyöristää ylös, jos on murto-osa) ja kerrottava se 10 dollarilla.
hankalinta on, kun ”pyöräytämme” osuuden seuraavasta 300 kilometristä. Voimme käyttää ”katto” funktiota (nimetään \(\left\lceil {} \right\rceil \)); tämä funktio antaa pienimmän kokonaisluvun, joka on suurempi tai yhtä suuri kuin sen tulo; esimerkiksi sekä 3.5: n että 4: n katto on 4.
näin meillä on:
\(\displaystyle F\left( x \right)=\left\{ \begin{array}{l}\text{ }50\text{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }0\le x\le 400\\ \ text{ }50+10\times \left\lceil {\frac{{x-400}}{{300}}} \oikea\rcil \ teksti{ }\,\,\,\,\,\,\text{ if }x>400\end{array} \right.\)
kokeillaan! Jos meillä on 1500 mailin matka, kustannukset olisivat \(\displaystyle 50 + 10\times \left\lceil {\frac{{1500-400}}{{300}}} \right\rceil \text{ }=50+10 \ times 4=\$90\).
ongelma:
mikä arvo \(\boldsymbol{a}\) tekisi tästä paloittain tehtävästä jatkuvan?
\(\displaystyle F\left( x \right)=\left\{ \begin{array}{l}3{{x}^{2}}+4\,\,\,\,\,\text{ if }x<-2\\5x + \boldsymbol{a}\,\,\,\,\,\,\,\,\teksti{if }x\ge -2\end{array} \right.\)
Solution:
jotta paloiteltu funktio olisi jatkuva, rajapisteessä (jossa funktio muuttuu) kahden \(y\) arvon on oltava samat. \ (X\) voidaan liittää -2 kummassakin funktiossa ja varmistaa, että\ (y\)’S: t ovat samat
\(\begin {align}3{{x}^{2}}+4&=5x+a\\3{{\left ({-2} \right)}^{2}}+4&=5\left( {-2} \right)+a\\12+4&=-10+a\\a&=26\end{align}\)
Jos \(a=26\), paloittain funktio on jatkuvia!
opettele nämä säännöt ja harjoittele, harjoittele, harjoittele!
more Practice: käytä alla olevaa Mathway-sovelmaa yrittääksesi kirjoittaa paloittain funktiota. Klikkaa Lähetä (sininen nuoli ongelman oikealla puolella) ja napsauta Kirjoita itseisarvo paloittain nähdäksesi vastauksen.
voit myös kirjoittaa oman ongelmasi, tai klikkaa oikeassa yläkulmassa olevia kolmea pistettä ja porata ”esimerkkejä” aiheittain.
Jos napsautat napauttamalla nähdäksesi vaiheet, tai klikkaa tästä, voit rekisteröityä Mathwayssa ilmaiseksi kokeiluversioon ja päivittää sitten maksulliseen tilaukseen milloin tahansa (saadaksesi minkä tahansa tyyppisen matematiikkaongelman ratkaistuksi!).
matriiseihin ja Ratkaisujärjestelmiin matriiseilla – olet valmis!