Konigsberg on preger-joen varrella sijaitseva kaupunki, joka 18. Kaupungin sisällä on kaksi saarta, jotka on yhdistetty rantaan seitsemällä sillalla (kuten alla).

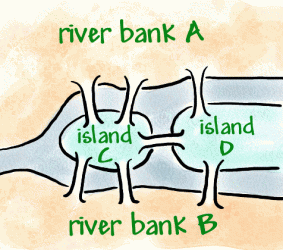
perinteeksi muodostui yrittää kävellä kaupungin ympäri tavalla, joka ylitti jokaisen sillan vain kerran, mutta se osoittautui vaikeaksi ongelmaksi. Leonhard Euler, sveitsiläinen matemaatikko Venäjän keisarinna Katariina Suuren palveluksessa, kuuli ongelmasta.Vuonna 1736 Euler todisti, että kävely ei ollut mahdollista tehdä. Heproved tämän keksimällä eräänlainen kaavio kutsutaan verkkoon, thatis koostuu vertices(pisteitä, joissa linjat täyttävät) ja kaaria (linjat).

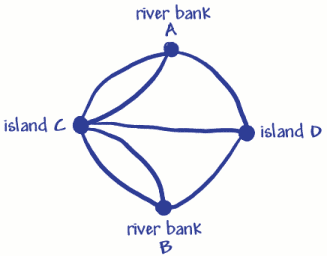
hän käytti kahta joentörmää ja kumpua neljää pistettä (kärkipistettä). Nämä on merkitty A, B ja C, D. seitsemän riviä(kaaria) ovat seitsemän siltaa. Näet, että 3 siltaa (kaaret)yhtyvät joentörmään A ja 3 yhtyvät joentörmään B. 5 siltaa (kaaret)yhtyvät saareen C ja 3 yhtyvät saareen D. Tämä tarkoittaa, että kaikki thevertices on pariton määrä kaaria, joten niitä kutsutaan oddvertices. (An jopa huippupiste olisi oltava parillinen määrä arcsjoining, se).
muista, että ongelmana oli kiertää kaupunkia ylittämässä jokainen silta vain kerran. On Euler verkon tämä tarkoitti jäljittämistä yli eacharc vain kerran, vierailevat kaikki vertices. Euler osoittautunut se ei voinut olla tehty, koska hän työskenteli, että on outoa huippupiste te wouldhave aloittaa tai lopettaa matkan että huippupiste. (Ajattele sitä).Koska siellä voi olla vain yksi alku ja yksi loppu, siellä voi vainbe kaksi outoa vertices jos aiot pystyä jäljittämään yli eacharc vain kerran. Koska silta ongelma on 4 outoa vertices, se justisn ’ t mahdollista tehdä! Mitä tapahtuu, jos ei ole outoa vertices atall? Voiko verkon jäljittää?

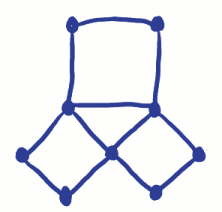
verkkojen keksiminen aloitti kokonaan uudenlaisen geometrian, jota kutsutaan termitopologiaksi. Topologiaa käytetään nykyään monin tavoin, muun muassa rautatieverkkojen suunnittelussa ja kartoituksessa. (Ahhh! Junien piti tulla sinne….)