- oppimistavoitteet
- painovoimaa vastaan tehty työ
- muunnos potentiaalienergian ja kineettisen energian välillä
- käyttäen potentiaalienergiaa laskelmien yksinkertaistamiseen
- Esimerkki 1. Putoamisen pysäyttävä voima
- strategia
- ratkaisu
- Keskustelu
- Esimerkki 2. Vuoristoradan nopeuden löytäminen sen korkeudesta
- strategia
- ratkaisu osaan 1
- solution for part 2
- Discussion and Implications
- Making Connections: Take-Home Investigation—Converting Potential to Kinetic Energy
- Sektion Yhteenveto
- käsitteelliset kysymykset
- ongelmat &harjoitukset
- Sanasto
- valitut ratkaisut ongelmiin & harjoitukset
oppimistavoitteet
tämän osion loppuun mennessä pystyt:
- selittämään gravitaatiopotentiaalienergian painovoimaa vastaan tehdyllä työllä.
- osoittavat, että gravitaatiopotentiaalienergia kappaleelle, jonka massa on m korkeudella H maapallolla, saadaan PEg = mgh.
- Näytä, miten tietoa potentiaalienergiasta aseman funktiona voidaan käyttää laskelmien yksinkertaistamiseen ja fysikaalisten ilmiöiden selittämiseen.
painovoimaa vastaan tehty työ
portaiden kiipeäminen ja esineiden nostaminen on työtä sekä tieteellisessä että arkisessa mielessä—se on työtä painovoimaa vastaan. Kun on työtä, tapahtuu energian muutos. Painovoimaa vastaan tehty työ liittyy tärkeään varastoituun energiaan, jota tutkimme tässä osiossa.

kuva 1. (a) painon nostamiseksi tehty työ varastoituu massa-maa-järjestelmään gravitaatiopotentiaalienergiana. B) kun paino liikkuu alaspäin, tämä gravitaatiopotentiaalienergia siirtyy käkikelloon.
laskemme työn, joka on tehty massan m kappaleen nostamisessa korkeuden h avulla, kuten kuvassa 1. Jos kappale nostetaan suoraan ylös vakionopeudella, sen nostamiseen tarvittava voima on yhtä suuri kuin sen paino mg. Massalle tehty työ on tällöin w = Fd = mgh. Määrittelemme tämän olevan gravitaatiopotentiaalienergia (PEg), joka on otettu objekti-maa-järjestelmään (tai saatu sillä). Tämä energia liittyy kahden toisiaan vetovoimalla vetävän kappaleen erotustilaan. Mukavuussyistä kutsumme tätä kappaleen saavuttamaksi Tappiksi ja tunnustamme, että tämä on energiaa, joka on varastoitunut maan gravitaatiokenttään. Miksi käytämme sanaa ”järjestelmä”? Potentiaalienergia on systeemin eikä yksittäisen kappaleen ominaisuus-johtuen sen fysikaalisesta sijainnista. Kappaleen gravitaatiopotentiaali johtuu sen sijainnista suhteessa ympäristöön maan ja kohteen järjestelmässä. Kappaleeseen kohdistuva voima on ulkoinen, systeemin ulkopuolelta tuleva voima. Kun se tekee positiivista työtä, se lisää systeemin gravitaatiopotentiaalienergiaa. Koska gravitaatiopotentiaalienergia riippuu suhteellisesta sijainnista, tarvitsemme vertailutason, jolla potentiaalienergia voidaan asettaa arvoon 0. Yleensä valitsemme tämän pisteen maan pinnaksi, mutta tämä piste on mielivaltainen; tärkeää on gravitaatiopotentiaalienergian ero, koska tämä ero liittyy tehtyyn työhön. Kappaleen gravitaatiopotentiaalienergian ero (maan ja kohteen järjestelmässä) kahden tikapuun välillä on sama kahdelle ensimmäiselle Puolalle kuin kahdelle viimeiselle Puolalle.
muunnos potentiaalienergian ja kineettisen energian välillä
Gravitaatiopotentiaalienergia voidaan muuntaa muiksi energiamuodoiksi, kuten kineettiseksi energiaksi. Jos vapautamme massan, gravitaatiovoima tekee sille mgh: n suuruisen työmäärän, jolloin sen liike-energia kasvaa samalla määrällä (työenergialauseella). Mielestämme on hyödyllisempää harkita vain PEg: n muuttamista KE: ksi ottamatta nimenomaisesti huomioon työn välivaihetta. (KS. Esimerkki 2.) Tämä pikanäppäin helpottaa ongelmien ratkaisemista energialla (jos mahdollista) eikä eksplisiittisesti voimilla.
tarkemmin määrittelemme gravitaatiopotentiaalienergian muutoksen ΔPEg: ksi = MGH: ksi, jossa yksinkertaisuuden vuoksi merkitsemme korkeuden muutosta h: lla tavanomaisen Δh: n sijaan. Huomaa, että H on positiivinen, kun lopullinen korkeus on suurempi kuin alkuperäinen korkeus, ja päinvastoin. Jos esimerkiksi käkikellosta ripustettu 0,500 kg: n massa nostetaan 1.00 m, niin sen gravitaatiopotentiaalienergian muutos on
\begin{array}{ll}mgh&&(0.500\text{ kg})(9.80\text{ m/S}^2)(1.00\text{ m})\\\text{ }&&4.90\text{ kg}\cdot\text{m}^2\Text{/S}^2=4.90\text{ j}\end{array}\\
huomaa, että gravitaatiopotentiaalienergian yksiköt osoittautuvat joules, sama kuin työ ja muut energiamuodot. Kun kello käy, massa laskee. Voimme ajatella massan vähitellen luopuvan 4.90 J gravitaatiopotentiaalienergiaa, ottamatta suoraan huomioon painovoimaa, joka tekee työn.
käyttäen potentiaalienergiaa laskelmien yksinkertaistamiseen

kuva 2. Gravitaatiopotentiaalienergian (ΔPEg) muutos pisteiden A ja B välillä on radasta riippumaton.
yhtälö ΔPEg = mgh koskee mitä tahansa polkua, jolla on h: n korkeuden muutos, ei vain silloin, kun massaa nostetaan suoraan ylöspäin. (KS. Kuva 2.) On paljon helpompaa laskea mgh (yksinkertainen kertolasku) kuin laskea monimutkaisella polulla tehty työ. Gravitaatiopotentiaalienergian ajatuksella on se kaksinkertainen etu, että se on hyvin laajasti sovellettavissa ja se helpottaa laskemista.
tästä eteenpäin katsomme, että massan m pystysuuntaisen sijainnin h muuttumiseen liittyy gravitaatiopotentiaalienergian MGH: n muutos, ja vältämme vastaavan mutta vaikeamman tehtävän laskea gravitaatiovoiman tekemä tai sitä vastaan tehty työ.
ΔPEg = mgh näiden kahden pisteen välisellä polulla. Gravitaatio on pieni voimaluokka, jossa voiman tekemä tai sitä vastaan tehty työ riippuu vain alku-ja päätepisteistä, ei niiden välisestä polusta.
Esimerkki 1. Putoamisen pysäyttävä voima
a 60.0-kg henkilö hyppää lattialle 3.00 m: n korkeudesta. jos hän laskeutuu jäykästi (polvinivelten puristuessa 0.500 cm: n verran), laske polvinivelten voima.
strategia
tämän henkilön energia nollaantuu tässä tilanteessa lattialle tehdystä työstä hänen pysähtyessään. Alkuperäinen tappi muuttuu ke kun hän putoaa. Lattian tekemä työ vähentää tämän liike-energian nollaan.
ratkaisu
lattiaan pysähtyneen henkilön tekemä työ merkitään w = Fd cos θ = −Fd miinusmerkillä, koska pysähtymisen aiheuttama siirtymä ja lattiasta tuleva voima ovat vastakkaisiin suuntiin (cos θ = cos 180º = -1). Lattia poistaa energiaa järjestelmästä, joten se tekee negatiivista työtä.
liike −energia, joka henkilöllä on lattialle päästyään, on korkeuden h: KE = −ΔPEg = – mgh pudotessa menetetty potentiaalienergian määrä.
henkilön polvien taivutusetäisyys d on paljon pienempi kuin putoamiskorkeus h, joten ylimääräinen gravitaatiopotentiaalienergian muutos polvitaipeen aikana jätetään huomioimatta.
lattian henkilölle tekemä työ w pysäyttää henkilön ja tuo henkilön liike −energian nollaan: W = – KE = mgh.
yhdistämällä tämä yhtälö lausekkeeseen W antaa −Fd = mgh.
muistaen, että h on negatiivinen, koska henkilö kaatui maahan, polviniveliin kohdistuvan voiman antaa
\displaystyle{F}=-\frac{mgh}{d}=-\frac{\left(60.0\text{ kg}\right)\left(9.80\text{ m/S}^2\right)\left(-3.00\text{ m}\right)}{5.00\times10^{-3}\text{ m}}=3.53\times10^5\text{ n}\\
Keskustelu
tällainen suuri voima (500 kertaa enemmän kuin henkilön paino) lyhyen törmäysajan aikana riittää murtakaa luita. Paljon parempi tapa pehmentää iskua on taivuttaa jalkoja tai vieriä maassa, jolloin voiman vaikutusaika pitenee. Taivutusliike 0,5 m tällä tavalla tuottaa voima 100 kertaa pienempi kuin esimerkissä. Kengurun hyppiminen osoittaa tämän menetelmän toiminnassa. Kenguru on ainoa suuri eläin, joka käyttää hyppimistä liikkumiseen, mutta hyppäämisen aiheuttamaa järkytystä vaimentaa sen takajalkojen taipuminen jokaisessa hypyssä. (KS. Kuva 3.)

kuva 3. Maan kengurulle tekemä työ vähentää sen liike-energian nollaan sen laskeutuessa. Kuitenkin kohdistamalla maahan voimaa takajalkoihin pidemmän matkan, vaikutus luihin vähenee. (luotto: Chris Samuel, Flickr)
Esimerkki 2. Vuoristoradan nopeuden löytäminen sen korkeudesta
- mikä on kuvassa 4 esitetty vuoristoradan lopullinen nopeus, jos se alkaa levosta 20,0 metrin mäen huipulta ja kitkavoimien tekemä työ on merkityksetöntä?
- mikä on sen lopullinen nopeus (olettaen jälleen mitättömän kitkan), jos sen alkunopeus on 5,00 m / s?
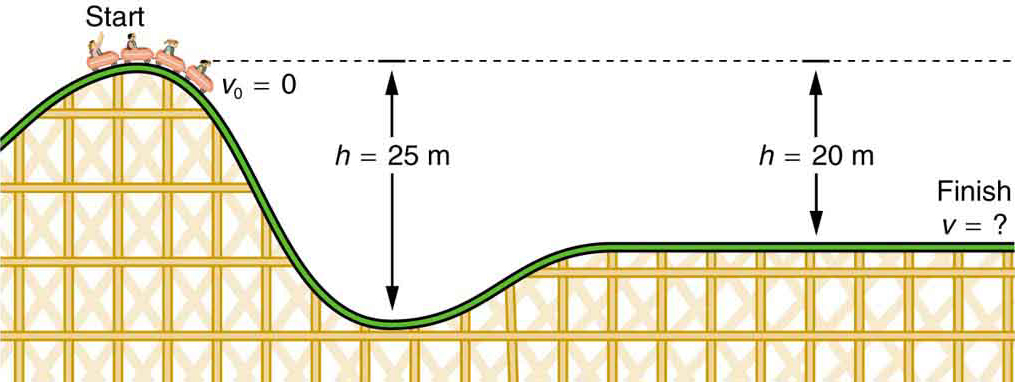
kuva 4. Vuoristoradan nopeus kasvaa, kun painovoima vetää sitä alamäkeen ja on suurimmillaan alimmillaan. Energian kannalta tarkasteltuna vuoristorata – maa-systeemin gravitaatiopotentiaalienergia muuttuu liike-energiaksi. Jos kitkan aikaansaama työ on merkityksetöntä, kaikki ΔPEg muuttuu ke: ksi.
strategia
vuoristorata menettää potentiaalienergiaa syöksyessään alamäkeen. Me laiminlyömme kitkan, niin että jäljellä voima kohdistetaan radan on normaali voima, joka on kohtisuorassa liikkeen suuntaan ja ei toimi. Vuoristoradan verkkotyöt tehdään sitten pelkän painovoiman avulla. Gravitaatiopotentiaalienergian menetys liikkuessaan alaspäin etäisyyden h läpi on yhtä kuin liike-energian lisäys. Tämä voidaan kirjoittaa yhtälömuodossa as-ΔPEg = ΔKE. Käyttämällä yhtälöt PEg ja KE, voimme ratkaista lopullinen nopeus v, joka on haluttu määrä.
ratkaisu osaan 1
tässä alkuperäinen kineettinen energia on nolla, joten \Delta\text{KE}=\frac{1}{2}MV^2\\\. Potentiaalienergian muutoksen yhtälön mukaan ΔPEg = mgh. Koska h on tässä tapauksessa negatiivinen, kirjoitamme tämän uudelleen ΔPEg = – mg|h| näyttääksemme miinusmerkin selvästi. Täten-ΔPEg = ΔKE muuttuu mg|h / =\frac{1}{2}{MV}^2\\.
ratkaisemalla V, huomaamme, että massa kumoaa ja että v=\sqrt{2G|h/}\\.
korvaavat tunnetut arvot,
\begin{array}{ll}v&&\sqrt{2\left(9.80\text{ m/s}^2\right)\left(20.0\text{ m}\right)}\\\text{ }&&19.8\text{ m/s}\end{array}\\
solution for part 2
again −δpeg=δke. Tällöin on olemassa alkuperäinen kineettinen energia, joten
\Delta\text{KE}=\frac{1}{2}MV^2-\frac{1}{2}mv_0^2\\\.
näin ollen mg|h / =\frac{1}{2}MV^2-\frac{1}{2}Mv_0^2\\.
järjestelemällä saadaan \frac{1}{2}MV^2=mg|h / +\frac{1}{2}MV+0^2\\.
tämä tarkoittaa, että lopullinen kineettinen energia on alkuperäisen kineettisen energian ja gravitaatiopotentiaalienergian summa. Massa kumoaa jälleen, ja v=\sqrt{2G|h / +v_0^2}\\.
tämä yhtälö on hyvin samanlainen kuin kinematiikan yhtälö v=\sqrt{v_0^2+2AD}\\, mutta se on yleisempi—kinematiikan yhtälö on voimassa vain vakiokiihtyvyydelle, kun taas yllä oleva yhtälö on voimassa mille tahansa polulle riippumatta siitä liikkuuko kappale vakiokiihtyvyydellä. Nyt tunnettujen arvojen korvaamisesta saadaan
\begin{array}{ll}v&&\sqrt{2\left(9.80\text{ m/s}^2\right)\left(20.0\text{ m}\right)+\left(5.00\text{ m/s}\right)^2}\\\text{ }&&20.4\text{ m/s}\end{array}\\
Discussion and Implications
huomaa ensin, että massa kumoaa. Tämä on melko yhdenmukaista putoavista kappaleista tehtyjen havaintojen kanssa, että kaikki kappaleet putoavat samalla nopeudella, jos kitka on häviävän pieni. Toiseksi otetaan huomioon vain vuoristoradan nopeus; sen suunnasta ei ole tietoa missään vaiheessa. Tämä paljastaa toisen yleisen totuuden. Kun kitka on mitätön, putoavan kappaleen nopeus riippuu vain sen alkunopeudesta ja korkeudesta eikä sen massasta tai kulkureitistä. Esimerkiksi vuoristoradan loppunopeus on sama riippumatta siitä, putoaako se 20,0 metriä suoraan alas vai kulkeeko se mutkikkaampaa polkua kuten kuvassa. Kolmanneksi, ja ehkä yllättäen, lopullinen nopeus osassa 2 on suurempi kuin osassa 1, mutta ylivoimaisesti alle 5,00 m/s. lopuksi, huomaa, että nopeus löytyy millä tahansa korkeudella matkan varrella yksinkertaisesti käyttämällä sopivaa arvoa h kiinnostavassa pisteessä.
olemme nähneet, että gravitaatiovoiman tekemä tai sitä vastaan tehty työ riippuu vain alku-ja päätepisteistä, eikä niiden välisestä polusta, minkä ansiosta voimme määritellä gravitaatiopotentiaalienergian yksinkertaistavan käsitteen. Voimme tehdä saman muutamille muille voimille, ja näemme, että tämä johtaa energian säilymislain muodolliseen määrittelyyn.
Making Connections: Take-Home Investigation—Converting Potential to Kinetic Energy
One can study the conversion of gravitational potential energy into kinetic energy in this experiment. Käytä sileällä, tasaisella pinnalla viivoitinta, jossa on pituudeltaan ura, ja kirjaa kaltevuuden tekemiseksi (KS.kuva 5). Aseta marmori viivoittimen 10 cm: n asentoon ja anna sen rullata viivoitin alas. Kun se osuu tasaiselle pinnalle, mittaa yhden metrin rullaamiseen kuluva aika. Aseta marmori 20 cm: n ja 30 cm: n kohtiin ja mittaa uudelleen 1 m: n rullaaminen tasaisella pinnalla. Etsi nopeus marmori tasolla pinnan kaikki kolme kantaa. Juoni nopeus potenssiin vs. matka kuljettu marmori. Mikä on kunkin juonen muoto? Jos muoto on suora, juoni osoittaa, että marmorin liike-energia pohjassa on verrannollinen sen potentiaalienergiaan vapautumispisteessä.

kuva 5. Marmori vierittää viivoittimen alas, ja sen nopeus tasaisella pinnalla mitataan.
Sektion Yhteenveto
- kappaleen nostamisessa painovoimaa vastaan tehdystä työstä tulee objekti-maa-systeemin potentiaalienergiaa.
- gravitaatiopotentiaalienergian muutos, ΔPEg, on ΔPEg = mgh, jossa h on korkeuden kasvu ja g painovoimasta johtuva kiihtyvyys.
- maan pinnan lähellä olevan kappaleen gravitaatiopotentiaalienergia johtuu sen sijainnista massa-maan järjestelmässä. Vain gravitaatiopotentiaalienergian eli ΔPEg: n eroilla on fysikaalinen merkitys.
- kappaleen laskeutuessa ilman kitkaa sen gravitaatiopotentiaalienergia muuttuu liike −energiaksi, joka vastaa kasvavaa nopeutta, niin että ΔKE = – ΔPEg
käsitteelliset kysymykset
- esimerkissä 2 laskimme vuoristoradan loppunopeuden, joka laskeutui 20 metrin korkeuteen ja jonka alkunopeus oli 5 m / s alamäkeen. Olettakaamme, että vuoristoradan alkunopeus olisi ollut 5 m/s ylämäkeen, ja se olisi noussut ylämäkeen, pysähtynyt ja rullannut sitten takaisin alas loppupisteeseen, joka on 20 m startin alapuolella. Siinä tapauksessa sillä oli sama loppunopeus. Selitä energian säästämisen kannalta.
- riippuuko se työ, jonka teet kirjan parissa, kun nostat sen hyllylle, valitusta polusta? – Missä ajassa? Hyllyn korkeudellako? Kirjan messusta?
ongelmat &harjoitukset
- vesivoimalaitos (katso kuva 6) muuntaa padon takana olevan veden gravitaatiopotentiaalienergian sähköenergiaksi. a) mikä on gravitaatiopotentiaalienergia suhteessa tilavuudeltaan 50 olevan järven generaattoreihin.0 km3 (massa = 5,00 × 1013 kg), kun otetaan huomioon, että järven keskikorkeus on 40,0 metriä generaattorien yläpuolella? B) vertaa tätä 9 megatonnin fuusiopommiin varastoituun energiaan.

kuva 6. Vesivoimalaitos(luotto: Denis Belevich, Wikimedia Commons)
- (a) kuinka paljon gravitaatiopotentiaalienergiaa (suhteessa maahan, jolle se on rakennettu) on varastoituna Kheopsin suureen pyramidiin, koska sen massa on noin 7 × 109 kg ja sen massakeskiö on 36.5 m maanpinnan yläpuolella? b) millaista tämä energia on verrattuna ihmisen päivittäiseen ravinnonsaantiin?
- Oletetaan, että 350-grammainen kookaburra (suuri kuningaskalastajalintu) poimii 75-grammaisen käärmeen ja nostaa sen 2,5 metriä maasta oksalle. a) miten paljon työtä lintu teki käärmeen hyväksi? b) miten paljon työtä se teki nostaakseen oman massakeskuksensa haaratoimistoon?
- esimerkissä 2 huomasimme, että 20,0 metriä laskeutuneen vuoristoradan nopeus oli vain hieman suurempi, kun sen alkunopeus oli 5,00 m / s kuin levosta lähtiessä. Tällöin ΔPE >> KEi. Vahvista tämä toteamus ottamalla ΔPE: n ja KEi: n suhde. (Huomaa, että massa kumoaa.)
- 100 gramman leluautoa liikuttaa puristettu jousi, joka käynnistää sen liikkumisen. Auto seuraa kaartuvaa rataa Kuvassa 7. Näytä, että leluauton lopullinen nopeus on 0,687 m/s, jos sen alkunopeus on 2,00 m/s ja se rannikko ylös kitkatonta rinnettä saaden 0,180 m korkeudessa.

kuva 7. Leluauto liikkuu ylös kaltevaa rataa. (luotto: Leszek Leszczynski, Flickr)
- alamäkihiihtokisassa yllättävän vähän etua saa juoksulähdön saamisesta. (Tämä johtuu siitä, että alkuperäinen liike-energia on pieni verrattuna gravitaatiopotentiaalienergian hyötyyn pienilläkin kukkuloilla.) Tämän osoittamiseksi etsi lopullinen nopeus ja aika, joka kuluu hiihtäjälle, joka skies 70.0 m pitkin 30º Rinne unohtamatta kitkaa: (a) alkaen levosta. b) alkunopeus on 2,50 m/s. c) yllättääkö vastaus? Keskustele siitä, miksi on edelleen edullista saada juoksulähtö hyvin kilpailluissa tapahtumissa.
Sanasto
gravitaatiopotentiaalienergia: energia, joka kappaleella On johtuen sen sijainnista gravitaatiokentässä
valitut ratkaisut ongelmiin & harjoitukset
1. (a) 1,96 × 1016 J; (b) järven gravitaatiopotentiaalienergian suhde pommiin varastoituneeseen energiaan on 0,52. Toisin sanoen järveen varastoitunut energia on noin puolet 9 megatonnin fuusiopommiin verrattuna.
3. a) 1, 8 J; b) 8, 6 j
5. {v}_{f} = \sqrt{2GH+{v_0}^2}=\sqrt{2\left(9.80\text{ m/s}^2\right)\left(-0.180\text{ m}\right)+\left(2.00\text{ m/s}\right)^2}=0.687\text{ m/s}\\