eksponenttifunktion ymmärtämisen jälkeen seuraava kohteemme on luonnollinen logaritmi.

ottaen huomioon, miten luonnollinen loki on kuvattu matematiikan kirjoissa, siinä ei ole juurikaan ”luonnollista”: se määritellään käänteiseksi $e^x$: ksi, joka on jo tarpeeksi outo eksponentti.

mutta siihen on tuore, intuitiivinen selitys: luonnollinen loki antaa tietyn kasvutason saavuttamiseen tarvittavan ajan.

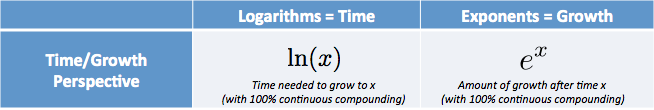
Oletetaan, että sinulla on sijoitus nallekarkkeihin (kukapa ei?), jonka korko on 100% vuodessa, kasvaa jatkuvasti. Jos haluat 10x kasvua, olettaen jatkuva yhdistäminen, voit odottaa vain $\ln (10)$ tai 2.302 vuotta. Etkö ymmärrä, miksi se kestää vain muutaman vuoden saada 10x kasvu? Etkö ymmärrä, miksi kuvio ei ole 1, 2, 4, 8? Lue lisää E.

E ja luonnollinen Loki ovat kaksosia:

• $e^x$ on summa, joka meillä on aloitettuamme 1.0 ja jatkuva kasvu $x$ aikayksiköille
• $\Ln(x)$ (luonnollinen logaritmi) on aika saavuttaa määrä $x$, olettaen että kasvoimme jatkuvasti 1.0: sta

ei liian paha, eikö? Samalla kun matemaatikot ryntäävät antamaan sinulle pitkän, teknisen selityksen, sukelletaan intuitiiviseen selitykseen.

E on kyse kasvusta

luku e on jatkuvasta kasvusta. Kuten näimme viime kerralla, $e^x$ avulla voimme yhdistää nopeus ja aika: 3 vuotta 100% kasvu on sama kuin 1 vuosi 300% kasvu, kun jatkuvasti pahentaa.

voimme ottaa minkä tahansa koron ja ajan yhdistelmän (50% 4 vuotta) ja muuntaa koron 100% mukavuussyistä (antaa meille 100% 2 vuotta). Muunnettaessa nopeudeksi 100%, meidän tarvitsee vain ajatella aikakomponenttia:

intuitiivisesti, $e^x$ tarkoittaa:

• kuinka paljon kasvua saan X-aikayksiköiden (ja 100% jatkuvan kasvun) jälkeen
• esimerkiksi: kolmen aikajakson jälkeen minulla on $E^3$ = 20,08 kertaa ”tavaraa”.

$e^x$ on skaalautuva tekijä, joka osoittaa kuinka paljon kasvua saisimme $x$ aikayksiköiden jälkeen.

Luonnollinen Loki on aikalailla

luonnollinen loki on käänteisarvo $e^x$, joka on hieno termi vastakohdalle. Hienostelusta puheen ollen latinankielinen nimi on logarithmus naturali, josta lyhenne ln.

Mitä tämä käänteinen tai vastakkainen juttu nyt tarkoittaa?

• $e^x$ antaa meidän kytkeä aikaa ja saada kasvua.
• $\Ln(x)$ avulla voimme kytkeä kasvun ja saada sen vaatiman ajan.

esimerkiksi:

• $e^3$ on 20,08. Kun 3 yksikköä aikaa, päädymme 20.08 kertaa sen, mitä aloitimme.
• $\Ln(20.08)$ on noin 3. Jos haluamme kasvua 20,08, odotamme 3 yksikköä aikaa (jälleen, olettaen 100% jatkuva kasvu).

kanssani? Luonnollinen hirsi antaa meille tarvittavan ajan halutun kasvun saavuttamiseen.

logaritminen aritmetiikka ei ole normaalia

olet tutkinut lokkeja aiemminkin, ja ne olivat outoja petoja. Miten kertolasku muutettiin yhteenlaskuksi? Jako vähennyslaskuun? Katsotaanpa.

mikä on $\LN(1)$? Intuitiivisesti, kysymys on: kuinka kauan odotan saada 1x minun nykyinen määrä?

nolla. Zip. Ei mitään. Olet jo 1x nykyinen määrä! Ei vie aikaa kasvaa 1: stä 1: een.

• $\Ln(1) = 0$

Ok, miten olisi murtoluku? Kuinka kauan saada 1/2 minun nykyinen määrä? Jos olet kasvanut jatkuvasti 100%, tiedämme, että $\Ln (2)$ on määrä aikaa kaksinkertaistua. Jos me kääntää sen (eli, ottaa negatiivinen aika) meillä olisi puolet nykyisestä arvosta.

• $\Ln(.5) = – \Ln(2)= -.693$

käy järkeen, eikö? Jos menemme taaksepäin .693 yksikköä (negatiivisia sekunteja, sanotaan) meillä olisi puolet nykyisestä määrästä. Yleensä voit kääntää murto – osan ja ottaa negatiivisen: $\Ln(1/3) = – \Ln(3) = -1,09$. Tämä tarkoittaa, että jos palaamme ajassa taaksepäin 1,09 yksikköä, meillä olisi kolmannes nykyisestä.

Ok, miten olisi negatiivisen luvun luonnollinen loki? Kuinka paljon aikaa kestää” kasvattaa ” bakteeripesäkkeesi 1: stä -3: een?

se on mahdotonta! Ei voi olla” negatiivista ” määrää bakteereja, eihän? Korkeintaan (tuota… vähintään) voi olla nolla, mutta ei ole mitään keinoa saada negatiivinen määrä pieniä otuksia. Negatiivisissa bakteereissa ei ole järkeä.

• $\Ln(\text{negative number}) = \text{undefined}$

määrittelemätön vain tarkoittaa ”ei ole aikaa, jota voit odottaa” saadakseen negatiivisen summan. (No, jos käytämme kuvitteellisia eksponentiaaleja, on olemassa ratkaisu. Mutta tänään pidetään se todellisena.)

logaritminen kertolasku on mahtava hauska

kuinka kauan kestää kasvaa 9x nykyinen määrä? Toki kelpaisi ln(9). Mutta se on liian helppoa, ollaan erilaisia.

voimme pitää 9x-kasvua kolminkertaistumisena (kun otetaan $\Ln (3)$ aikayksikköä) ja sitten kolminkertaistumisena uudelleen (kun otetaan toinen $\Ln(3)$ aikayksikköä):

• Time to grow 9x = $\Ln(9)$ = Time to triple and triple again = $\Ln(3) + \Ln(3)$

mielenkiintoinen. Mitä tahansa kasvulukua, kuten 20, voidaan pitää 2x-kasvuna, jota seuraa 10x-kasvu. Tai 4-kertainen kasvu, jota seuraa 5-kertainen kasvu. Tai 3x kasvu seuraa 6.666 X kasvu. Näetkö kuvion?

• $\Ln(a*b) = \ln(a) + \Ln(b)$

a ajan loki b = loki(a) + loki(b). Tässä suhteessa on järkeä, kun ajattelee kasvuaikaa.

Jos haluamme kasvaa 30x, voimme odottaa $\Ln(30)$ kerralla, tai yksinkertaisesti odottaa $\Ln(3)$, kolminkertaistaa, sitten odottaa $\ln(10)$, kasvaa 10x uudelleen. Nettovaikutus on sama, joten nettoajan pitäisi olla sama myös (ja se on).

entäs jako? $\Ln(5/3)$ tarkoittaa: kuinka kauan kestää kasvaa 5 kertaa ja sitten ottaa 1/3 siitä?

no, kasvaminen 5 kertaa on $\LN(5)$. Kasvava 1/3 on $ – \LN (3)$ aikayksikköä. Joten

• $\Ln(5/3) = \Ln(5) – \Ln(3)$

, joka sanoo: kasva 5 kertaa ja ”mene ajassa taaksepäin”, kunnes sinulla on kolmannes tuosta määrästä, joten sinulle jää 5/3 kasvua. Yleensä meillä on

• $\Ln (a/b) = \ln (a) – \Ln(b)$

toivon, että logaritmien outo matematiikka alkaa olla järkevää: kasvun kertolasku muuttuu ajan yhteenlaskuksi, kasvun jakaminen ajan vähennykseksi. Älä opettele sääntöjä ulkoa, vaan ymmärrä ne.

käyttämällä luonnollisia tukkeja millä tahansa nopeudella

”Toki”, sanot, ”tämä tukkijuttu toimii 100%: n kasvuun, mutta entä se 5%, jonka normaalisti saan?”

It ’ s no problem. ”Aika ”saamme takaisin $\LN()$ on itse asiassa yhdistelmä korko ja aika,” x ” meidän $e^x$ yhtälö. Me vain oletamme 100% tehdä siitä yksinkertaista, mutta voimme käyttää muita numeroita.

Oletetaan, että haluamme 30x kasvua: plug in $\Ln(30)$ ja saamme 3.4. Tämä tarkoittaa:

• $e^x = \text{growth}$
• $e^{3.4} = 30$

ja intuitiivisesti tämä yhtälö tarkoittaa ”100%: n tuotto 3,4 vuodeksi on 30x kasvu”. Yhtälön voidaan katsoa olevan:

voimme muokata ”nopeutta” ja ”aikaa”, kunhan korko * aika = 3,4. Oletetaan esimerkiksi, että haluamme 30x kasvua – kuinka kauan odotamme olettaen, että 5% tuotto?

• $\Ln(30) = 3,4$
• $\text{rate} * \text{time} = 3.4$
• $.05 * \text{time} = 3.4$
• $\text{time} = 3.4/.05 = 68 \text{years}$

intuitiivisesti ajattelen ”$\Ln(30) = 3,4$, joten 100% kasvu vie 3,4 vuotta. Jos kaksinkertaistan kasvuvauhdin, puolitan tarvittavan ajan.”

• 100% 3, 4 vuotta = 1, 0 * 3, 4 = 3, 4
• 200% 1, 7 vuotta = 2, 0 * 1, 7 = 3, 4
• 50% 6, 8 vuotta = 0, 5 * 6, 8 = 3, 4
• 5% 68 vuotta = .05 * 68 = 3,4

Cool, eh? Luonnollista lokia voi käyttää millä tahansa korolla tai ajalla, kunhan niiden tuote on sama. Voit heilutella muuttujia niin paljon kuin haluat.

mahtava esimerkki: 72: n sääntö

72: n sääntö on mentaalinen matematiikan oikotie, jolla voi arvioida rahojen tuplaamiseen tarvittavan ajan. Me aiomme saada sen (JEE! ja vielä parempi, me aiomme ymmärtää sen intuitiivisesti.

kuinka kauan kestää tuplata rahasi 100 prosentin korolla joka vuosi?

Uh oh. Olemme käyttäneet luonnollista lokia jatkuviin korkoihin, mutta nyt pyydät vuosikorkoa? Eikö tämä sotke kaavaamme? Kyllä, se tulee, mutta kohtuullisilla koroilla, kuten 5%, 6% tai jopa 15%, ei ole paljon eroa vuosittaisen yhteenlasketun ja täysin jatkuvan koron välillä. Karkea kaava toimii suurin piirtein ja teeskentelemme, että saamme jatkuvaa kiinnostusta.

nyt kysymys on helppo: kuinka kauan tuplata 100 prosentin korolla? ln (2)= .693. Se kestää .693 aikayksikköä (vuotta, tässä tapauksessa) kaksinkertaistaa rahaa jatkuva yhteenlasku kanssa korko 100%.

Ok, entä jos korkomme ei ole 100% entä jos se on 5% tai 10%?

yksinkertainen. Niin kauan kuin korko * aika = .693, tuplaamme rahamme:

• rate * time = .693
• time = .693/korko

joten jos meillä olisi vain 10% kasvu, se veisi .693 / .10 tai 6,93 vuotta tuplaan.

asioiden yksinkertaistamiseksi kerrotaan 100: lla, jotta voidaan puhua sijasta 10: stä .10:

• time to double = 69,3 / rate, jossa koron oletetaan olevan prosentteina.

nyt aika kaksinkertaistua 5 prosentin kasvulla on 69,3 / 5 tai 13,86 vuotta. Kuitenkin, 69.3 ei ole kaikkein jaollinen luku. Valitaan lähinaapuri, 72, jonka voi jakaa 2, 3, 4, 6, 8 ja monta muuta numeroa.

• aika tuplata = 72/korko

mikä on sääntö 72! Rauhallisesti.

Jos haluat löytää triplausajan, käytä Ln(3) ~ 109,8: aa ja saat

• aika triplaan = 110/rate

, mikä on toinen hyödyllinen nyrkkisääntö. Sääntö 72 on hyödyllinen korkojen, väestönkasvun, bakteeriviljelmien ja kaiken, mikä kasvaa eksponentiaalisesti.

minne täältä?

toivon, että luonnon loki on järkevämpi — se kertoo, kuinka paljon aikaa tarvitaan mihin tahansa eksponentiaaliseen kasvuun. Pidän sitä ”luonnollisena”, koska e on yleinen kasvunopeus, joten ln: ää voidaan pitää” universaalina ” tapana selvittää, kuinka kauan kasvu kestää.

kun näet $\Ln(x)$, ajattele vain ”kuinka paljon aikaa kasvaa X: ksi”. Seuraavassa kirjoituksessa yhdistämme e: n ja ln: n, ja matematiikan makea tuoksu täyttää ilman.

Liite: E: n luonnollinen Loki

Quick quiz: What ’ s $\Ln (e)$?

• matematiikkarobotti sanoo: koska ne on määritelty käänteisfunktioiksi, selvästi $\ln (e) = 1$
• intuitiivinen ihminen: ln (e) on aika, joka kuluu ”e”: n kasvuyksiköiden saamiseen (noin 2,718). Mutta E on kasvun määrä 1 aikayksikön jälkeen, joten $\ln (e) = 1$.

ajattele intuitiivisesti.

muita julkaisuja tässä sarjassa

1. Eksponenttifunktioiden intuitiivinen opas & e
2. luonnollisen logaritmin (Ln) Demystifiointi
3. visuaalinen opas yksinkertaisiin, yhdistettyihin ja jatkuviin korkoihin
4. E: n yhteiset määritelmät (väritetty)
5. eksponenttien ymmärtäminen (miksi 0^0 = 1?)
6. käyttäen logaritmeja reaalimaailmassa
7. miten ajatella eksponenttien ja logaritmien kanssa
8. ymmärtäen diskreetin vs. jatkuvan kasvun
9. mitä eksponentti todella tarkoittaa?
10. Q: Miksi e on erityinen? (2.718… ei 2: ta, 3.7: ää tai muuta numeroa?)