muissa jaksoissa mainittiin, että monet kiinteiden aineiden, nesteiden ja kaasujen ominaisuuksista voitaisiin ottaa huomioon, jos oletamme, että aineet koostuvat atomeista tai molekyyleistä, jotka ovat jatkuvasti liikkeessä. Boylen laki ja muut kaasulait ovat nyt antaneet meille paljon enemmän kvantitatiivista tietoa kaasuista, ja on syytä kysyä, voimmeko edellisen mallin avulla tehdä määrällisiä ennusteita näiden lakien mukaisesti. Vastatessamme tähän kysymykseen saamme myös tärkeitä tietoja lämpötilan ja lämpöenergian luonteesta.

molekyyliliikkeeseen perustuvaa kaasun käyttäytymisen mikroskooppiteoriaa kutsutaan kaasujen kineettiseksi teoriaksi. Sen peruspostulaatit on lueteltu taulukossa 1:

taulukko \(\PageIndex{1}\) kaasujen kineettisen teorian postulaatit.

1 kaasun molekyylit ovat pieniä ja hyvin kaukana toisistaan. Suurin osa kaasun tilavuudesta on tyhjää tilaa.

2 kaasumolekyyliä on jatkuvassa satunnaisessa liikkeessä. Yhtä monta molekyyliä liikkuu yhteen suuntaan kuin mihin tahansa muuhunkin.

3 molekyyliä voi törmätä toisiinsa ja säiliön seinämiin. Törmäykset seiniin selittävät kaasun paineen.

4 törmäyksissä molekyylit eivät menetä liike-energiaa; toisin sanoen törmäysten sanotaan olevan täysin kimmoisia. Kaikkien molekyylien yhteenlaskettu liike-energia pysyy vakiona, ellei

5: n kanssa ole jonkin verran ulkopuolista häiriötä, molekyylit eivät aiheuta toisiinsa houkuttelevia tai vastenmielisiä voimia muutoin kuin törmäysprosessin aikana. Törmäysten välillä ne liikkuvat suorina linjoina.

niistä on mahdollista johtaa seuraava lauseke kaasun paineelle sen molekyylien ominaisuuksien suhteen:

\ missä P, V = kaasun paine ja tilavuus

n = molekyylien lukumäärä

m = kunkin molekyylin massa

(u2)ave = kaikkien yksittäisten molekyylin nopeuksien neliöiden keskiarvo (tai keskiarvo). Tätä keskimääräistä neliönopeutta on käytettävä, koska paine on verrannollinen molekyylin nopeuden neliöön, ja molekyylien törmäykset aiheuttavat eri molekyyleille aivan erilaiset nopeudet.

sen sijaan, että keskittyisimme Eq: n laatimismenettelyyn. \(\ref{1}\), tarkastelkaamme yhtälöä ja varmistakaamme, että sen yleiset ominaisuudet ovat paljolti odotusten mukaiset. Jollakin tavalla kyky tehdä tämä kaavalla on hyödyllisempi kuin kyky johtaa se. Kuva \(\PageIndex{1}\)

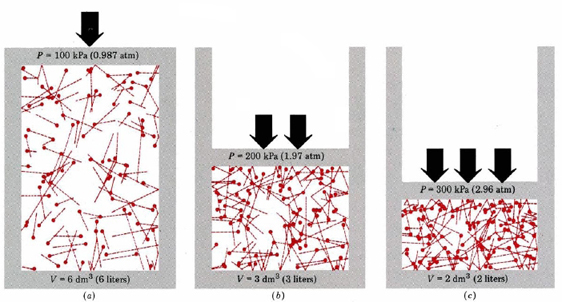ensinnäkin yhtälö kertoo, että kaasun paine on verrannollinen molekyylien määrään jaettuna tilavuudella. Tämä on esitetty graafisesti Kuvassa \(\PageIndex{1}\), jossa tietokone on piirtänyt saman määrän kaasumolekyylejä, joilla on kullakin kolme eri volyymia. Kunkin molekyylin ”häntä” näyttää tarkan reitin, jota kyseinen molekyyli seurasi edellisen mikrosekunnin aikana—mitä pidempi häntä, sitä nopeammin molekyyli kulki. Pyrstön pituuksien neliöiden keskiarvo on verrannollinen (u2)ave: hen ja on sama kaikissa kolmessa diagrammissa. Oletetaan myös, että kaikilla molekyyleillä on yhtä suuret massat.

kuten näette, kaasun tilavuuden pienentäminen lisää törmäysten määrää pinta-alayksikköä kohti säiliön seinissä. Jokainen törmäys kohdistuu seinään; voima pinta-alayksikköä kohti on paine, joten törmäysten määrä pinta-alayksikköä kohti on verrannollinen paineeseen. Määrän puolittaminen kaksinkertaistaa paineen, ennustus, joka on yhtäpitävä Boylen laissa tiivistettyjen kokeellisten tosiasioiden kanssa. Yhtälö \(\ref{1}\) kertoo myös, että paine on verrannollinen kunkin kaasumolekyylin massaan. Tämäkin on odotettavissamme. Raskaat molekyylit antavat suuremman ”työntövoiman”(tekninen termi tälle on impulssi) seinää vasten kuin kevyet, joilla on sama nopeus.

lopulta yhtälö kertoo, että paine on verrannollinen molekyylin nopeuksien neliöiden keskiarvoon. Tämä riippuvuus nopeuden neliöstä on kohtuullinen, jos ymmärrämme, että molekyylin nopeuden kaksinkertaistamisella on kaksi vaikutusta.

ensinnäkin molekyyli voi edetä pidemmälle tietyn pituisessa ajassa, jolloin seinämien törmäysten määrä kaksinkertaistuu. Tämä kaksinkertaistaisi paineen. Toiseksi molekyylin nopeuden kaksinkertaistaminen kaksinkertaistaa jokaisen törmäyksen työntövoiman tai impulssin. Tämä kaksinkertaistaa paineen uudelleen. Siksi molekyylin nopeuden kaksinkertaistaminen nelinkertaistaa paineen, ja suurelle joukolle molekyylejä P on verrannollinen neliönopeuden keskiarvoon.