Atomiorbitaalit
orbitaali on Bohrin radan kvanttimekaaninen hienosäätö. Toisin kuin hänen käsityksensä yksinkertaisesta ympyräradasta, jonka säde on kiinteä, orbitaalit ovat matemaattisesti johdettuja avaruuden alueita, joilla on erilaiset todennäköisyydet saada elektroni.
yksi tapa esittää elektronien todennäköisyysjakaumia on esitetty kuvassa 6.5.2 vedyn 1s-orbitaalille. Koska Ψ2 antaa todennäköisyyden elektronin löytymiselle tietyssä avaruuden tilavuudessa (kuten kuutiometrissä), Ψ2 vs. etäisyys ytimestä (r) on todennäköisyystiheyden kuvaaja. 1s-orbitaali on pallosymmetrinen, joten todennäköisyys löytää 1s-elektroni missä tahansa pisteessä riippuu vain sen etäisyydestä ytimestä. Todennäköisyystiheys on suurin R = 0 (ytimessä) ja pienenee tasaisesti etäisyyden kasvaessa. Hyvin suurilla R-arvoilla elektronin todennäköisyystiheys on hyvin pieni, mutta ei nolla.
sen sijaan voimme laskea säteittäisen todennäköisyyden (todennäköisyys löytää 1s elektroni etäisyydellä R ytimestä) laskemalla yhteen todennäköisyydet, että elektroni on kaikissa pisteissä sarjassa X pallomaisia kuoria, joiden säde on r1, r2, r3,…, rx − 1, RX. Itse asiassa, olemme jakamalla atomi hyvin ohut samankeskinen kuoret, paljon kuin kerrokset sipuli (osa (A) Kuvassa \(\PageIndex{1}\)), ja laskemalla todennäköisyys löytää elektroni kunkin pallomainen kuori. Muista, että elektronin todennäköisyystiheys on suurin pisteessä R = 0 (Osa (B) Kuvassa \(\PageIndex{1}\)), joten pisteiden tiheys on suurin pienimmillä pallomaisilla kuorilla Kuvassa \(\PageIndex{1}\). Sen sijaan kunkin pallomaisen kuoren pinta-ala on yhtä suuri kuin 4nr2, joka kasvaa hyvin nopeasti r: n kasvaessa (osa (C) Kuvassa \(\PageIndex{1}\)). Koska pallokuorten pinta-ala kasvaa nopeammin r: n kasvaessa kuin elektronin todennäköisyystiheys pienenee, säteittäisen todennäköisyyden kuvaajalla on maksimi tietyllä etäisyydellä (osa (D) Kuvassa \(\PageIndex{1}\)). Tärkeintä on, että kun R on hyvin pieni, pallomaisen kuoren pinta-ala on niin pieni, että elektronin löytämisen kokonaistodennäköisyys ytimen lähellä on hyvin pieni; ytimessä elektronin todennäköisyys katoaa (osa (D) Kuvassa \(\PageIndex{1}\)).

vetyatomille radiaalisen todennäköisyyslaskennan huippu tapahtuu pisteessä r = 0,529 Å (52,9 pm), joka on täsmälleen Bohrin N = 1-kiertoradalle laskema säde. Näin kvanttimekaniikasta saatu todennäköisin säde on identtinen klassisen mekaniikan laskeman säteen kanssa. Bohrin mallissa elektronin oletettiin kuitenkin olevan tällä etäisyydellä 100% ajasta, kun taas kvanttimekaanisessa Schrödingerin mallissa se on tällä etäisyydellä vain osan ajasta. Ero näiden kahden mallin välillä johtuu elektronin aaltomaisesta käyttäytymisestä ja Heisenbergin epävarmuusperiaatteesta.
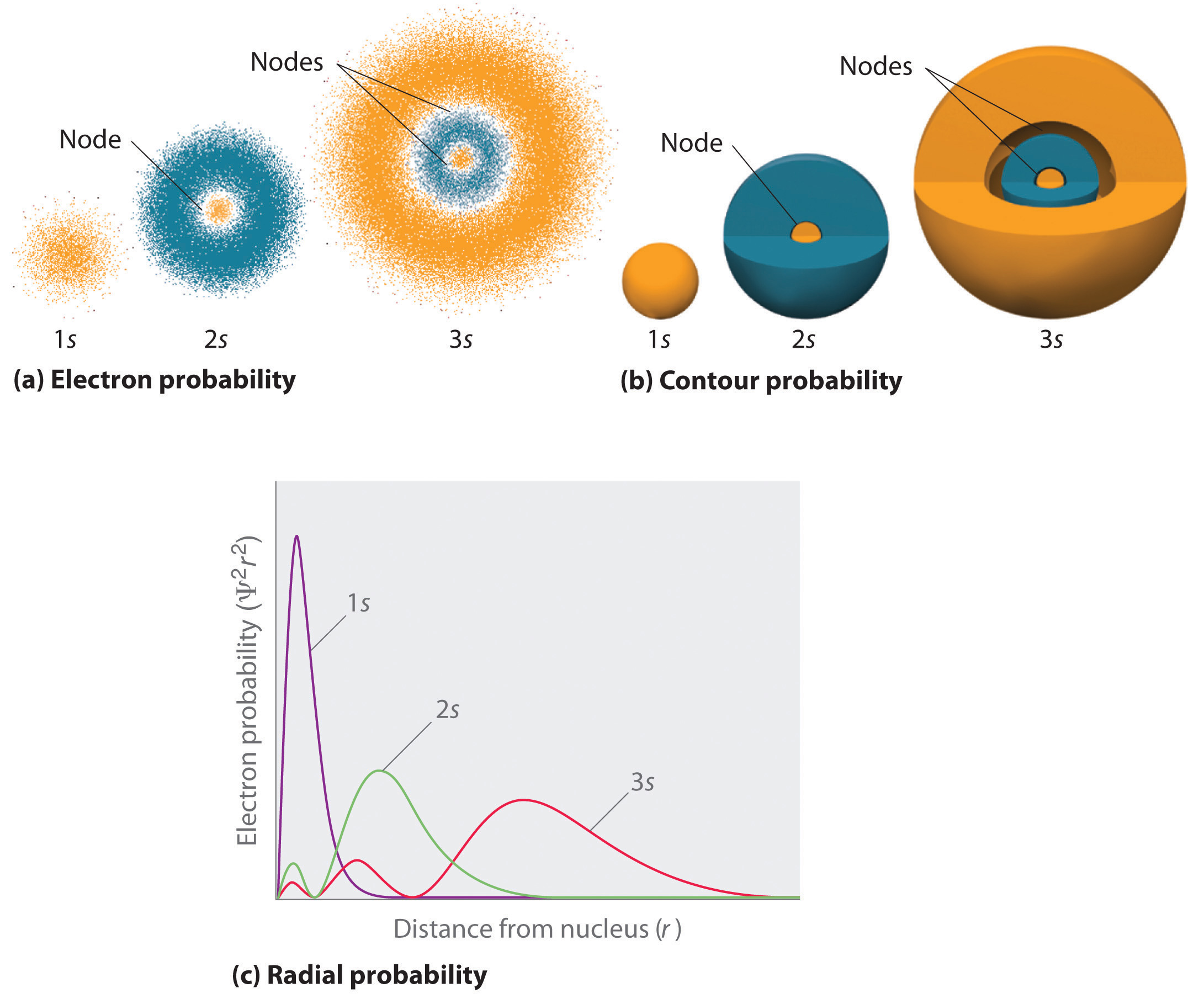
kuva \(\PageIndex{2}\) vertaa elektronien todennäköisyystiheyksiä vedyn 1s -, 2s-ja 3s-orbitaaleille. Huomaa, että kaikki kolme ovat pallosymmetrisiä. 2s – ja 3s-orbitaaleilla (ja myös kaikilla muilla s-orbitaaleilla) elektronin todennäköisyystiheys ei kuitenkaan putoa tasaisesti r: n kasvaessa. sen sijaan säteittäisillä todennäköisyyspiireillä havaitaan sarja minimejä ja maksimeja (osa (C) Kuvassa \(\PageIndex{2}\)). Minimit vastaavat pallomaisia solmuja (nollaelektronitodennäköisyyden alueita), jotka vuorottelevat nollaelektronitodennäköisyyden pallomaisten alueiden kanssa.