Purplemath
i matematik er en “identitet” en ligning, der altid er sand. Disse kan være” trivielt “sande, som” H = H “eller nyttigt sande, såsom Pythagoras sætning ‘s” a2 + b2 = c2 ” for højre trekanter. Der er masser af trigonometriske identiteter, men følgende er dem, du mest sandsynligt vil se og bruge.
Basic & Pythagorean, Angle-Sum & -Difference, Double-Angle, Half-Angle, Sum, Product
Content Continues Below
MathHelp.com
Need a custom math course?
K12 | College | Test Prep

Grundlæggende og Pythagoræiske Identiteter
Affiliate
læg Mærke til, hvordan en “co-(noget)”trig-forhold altid er den reciprokke af nogle “ikke-samarbejde” forhold. Du kan bruge denne kendsgerning til at hjælpe dig med at holde lige, at cosecant går med sinus og secant går med cosinus.
følgende (især den første af de tre nedenfor) kaldes “Pythagoras” identiteter.
sin2 (t) + cos2 (t) = 1
tan2(t) + 1 = sec2 (t)
1 + cot2 (t) = csc2 (t)
annonce
Bemærk, at de tre identiteter frem for alt involverer kvadrering og antallet af 1. Du kan se forholdet mellem Pythagoras og Thereom klart, hvis du overvejer enhedscirklen, hvor vinklen er t, den “modsatte” side er synd(t) = y, den “tilstødende” side er cos(t) = h, og hypotenusen er 1.
Vi har yderligere identiteter relateret til trig–forholdets funktionelle status:
sin (–t) = –sin(t)
cos (–t) = cos(t)
tan (–t) = -tan(t)
Bemærk især, at sinus og tangent er ulige funktioner, idet de er symmetriske om oprindelsen, mens cosinus er en jævn funktion, idet de er symmetriske om Y-aksen. Det faktum, at du kan tage argumentets “minus” tegn udenfor (for sinus og tangent) eller eliminere det helt (for cosinus) kan være nyttigt, når du arbejder med komplicerede udtryk.
Vinkel-Sum og -Forskel Identiteter
sin(α + β) = sin(α) cos(β) + cos(α) sin(β)
sin(α – β) = sin(α) cos(β) – cos(α) sin(β)
cos(α + β) = cos(α) cos(β) – sin(α) sin(β)
cos(α – β) = cos(α) cos(β) + sin(α) sin(β)
Ved den måde, i ovenstående identiteter, vinkler er angivet med græske bogstaver. A-type bogstavet, “Kris”, kaldes” alpha”, som udtales”AL-fuh”. B-type bogstavet, “Kris”, kaldes” beta”, som udtales”BAY-tuh”.
indhold fortsætter under
Dobbeltvinkelidentiteter
sin(2 gange) = 2 gange) cos(gang)
cos(2 gange) = cos2(gang)-sin2(gang) = 1 – 2 sin2(gang) = 2 cos2(gang) – 1
halv – vinkelidentiteter
ovenstående identiteter kan angives igen ved at kvadrere hver side og fordoble alle vinkelmålinger. Resultaterne er som følger:
Affiliate

Sum Identities
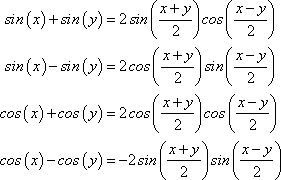
Product Identities
affiliate
du vil bruge alle disse identiteter, eller næsten så, for at bevise andre trig identiteter og til at løse trig ligninger. Men hvis du fortsætter med at studere calculus, skal du være særlig opmærksom på de omformulerede sinus-og cosinus-halvvinkelidentiteter, fordi du bruger dem meget i integreret beregning.
URL: https://www.purplemath.com/modules/idents.htm
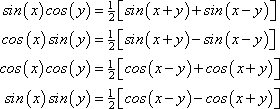 sin(s)cos(y)=(1/2), cos(s)sin(y)=(1/2), cos(s)cos(y)=(1/2), sin(S)sin(y)=(1/2)
sin(s)cos(y)=(1/2), cos(s)sin(y)=(1/2), cos(s)cos(y)=(1/2), sin(S)sin(y)=(1/2)