dette afsnit dækker:

• Introduktion til stykkevis funktioner
• evaluering af stykkevis funktioner
• graftegning stykkevis funktioner
• Sådan fortæller du, om en stykkevis funktion er kontinuerlig eller ikke-kontinuerlig
• indhentning af ligninger fra stykkevis funktionsgrafer
• absolut værdi som stykkevis funktion
• transformationer af stykkevis funktioner
• stykkevis funktion ordproblemer
• mere praksis

li>

stykkevis funktioner (eller stykkevis funktioner) er lige hvad de hedder: stykker af forskellige funktioner (underfunktioner) alt på en graf. Den nemmeste måde at tænke på dem er, hvis du tegnede mere end en funktion på en graf, og du bare slettede dele af funktionerne, hvor de ikke skulle være (langs \(h\) s); de er defineret forskelligt for forskellige intervaller af \(H\). vi bruger \(\) til at finde ud af, hvilket interval det er i, så vi kan finde ud af, hvad \(y\) skal være.

Bemærk, at der er et eksempel på en stykkevis funktions inverse her i afsnittet inverser af funktioner.

Here’s an example and graph:

Piecewise Function

Graph

\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ if }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ if }x>-2\end{align} \right.\) (Der er andre måder at vise dette på, såsom at bruge et “for” i stedet for et “if” og bruge kommaer eller halvkoloner i stedet for “if”.) domæne: \(\mathbb{R},\,\,\, \ tekst{eller}\,\, \ left ({- \infty, \ infty } \ right)\) rækkevidde: \(\mathbb{R},\,\,\,\tekst{eller}\,\,\venstre( {-\infty ,\infty } \højre)\)

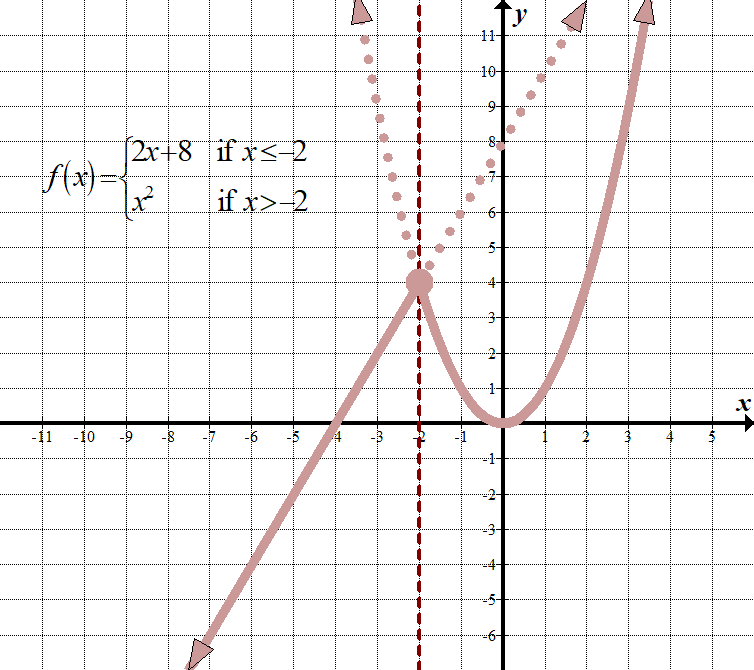hvad dette betyder er for hver \(h\) mindre end eller lig med -2, skal vi tegne linjen \(2H+8\), som om det var den eneste funktion på grafen. For hver \(h\) værdi større end -2, skal vi graf \({{H}^{2}}\), som om det var den eneste funktion på grafen. Så er vi nødt til at “slippe af med” de dele, som vi ikke har brug for. Husk, at vi stadig bruger oprindelsen som referencepunkt for begge grafer!

se hvordan den lodrette linje \(H=-2\) fungerer som en “grænse” linje mellem de to grafer?

Bemærk, at punktet \((-2,4)\) har en lukket cirkel på den. Teknisk set bør det kun tilhøre funktionen \(2H+8\), da denne funktion har mindre end eller lighedstegn, men da punktet også er på grafen \({{H}^{2}}\), kan vi bare bruge en lukket cirkel, som om den vises på begge funktioner. Ikke så slemt, vel?

evaluering af stykkevis funktioner

Nogle gange får du stykkevis funktioner og bliver bedt om at evaluere dem; med andre ord skal du finde \(y\) værdierne, når du får en \(h\) værdi. Lad os gøre dette for \(H=-6\) og \(H=4\) (uden at bruge grafen). Her er funktionen igen:

\(\displaystyle f \ left (\right)= \ left \ {\begin{align}2+8\,\,\,\,\,&\tekst{ hvis } \ \ le -2 \ \ {{}^{2}}\,\,\,\,\,\,\,\ tekst { }\, &\tekst{ hvis}>-2\end{juster} \højre.\)

vi vil først se på betingelserne til højre først for at se, hvor vores \(H\) er. Når \(h=-6\), ved vi, at det er mindre end -2, så vi tilslutter kun vores \(H\) til \(2H+8\). \(f)\) eller \(y\) er \((2)(-6)+8=-4\). Vi er ikke engang interesserede i \(\boldsymbol{{2}}\)! Det er så nemt. Du kan også se, at vi gjorde dette korrekt ved hjælp af grafen ovenfor.

prøv nu \(4\). Vi ser først på det rigtige og ser, at vores \(H\) er større end -2, så vi sætter det i \({{H}^{2}}\). (Vi kan bare ignorere \(2 gange + 8\) denne gang.) \(f)\) eller \(y\) er \({{4}^{2}}=16\).

graftegning stykkevis funktioner

du vil sandsynligvis blive bedt om at tegne stykkevis funktioner. Nogle gange indeholder graferne funktioner, der ikke er kontinuerlige eller diskontinuerlige, hvilket betyder, at du skal hente din blyant midt i grafen, når du tegner den (som et spring!). Kontinuerlige funktioner betyder, at du aldrig behøver at hente din blyant, hvis du skulle tegne dem fra venstre mod højre.

og husk, at graferne kun er sande funktioner, hvis de består den lodrette Linjetest.

lad os tegne disse stykkevis funktioner og afgøre, om de er kontinuerlige eller ikke-kontinuerlige. Bemærk, hvordan vi tegner hver funktion, som om den var den eneste, og derefter “sletter” de dele, der ikke er nødvendige. Vi får også domænet og rækkevidden som vi gjorde her i afsnittet algebraiske funktioner.

Piecewise Function	Graph
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\left( {0,\infty } \right)\)
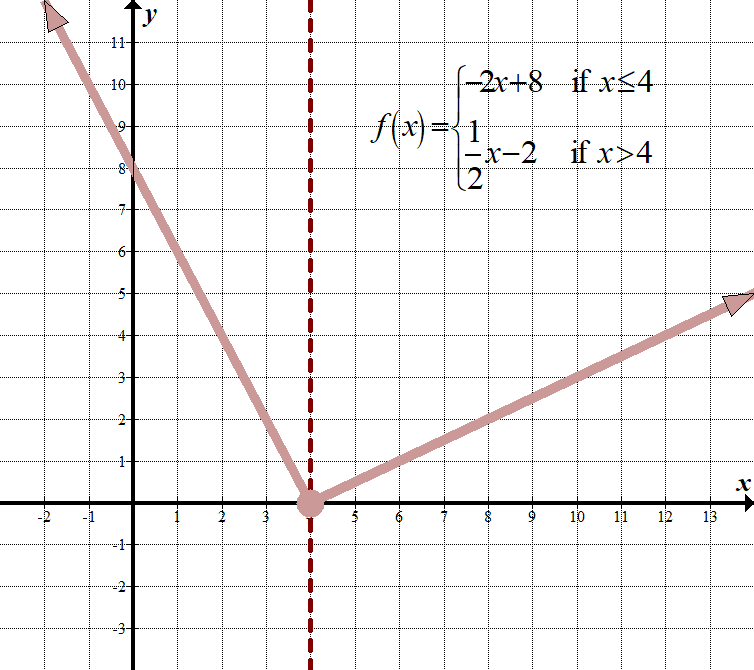\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1}\le x<4\\x-5\,\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\) Non-Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\)

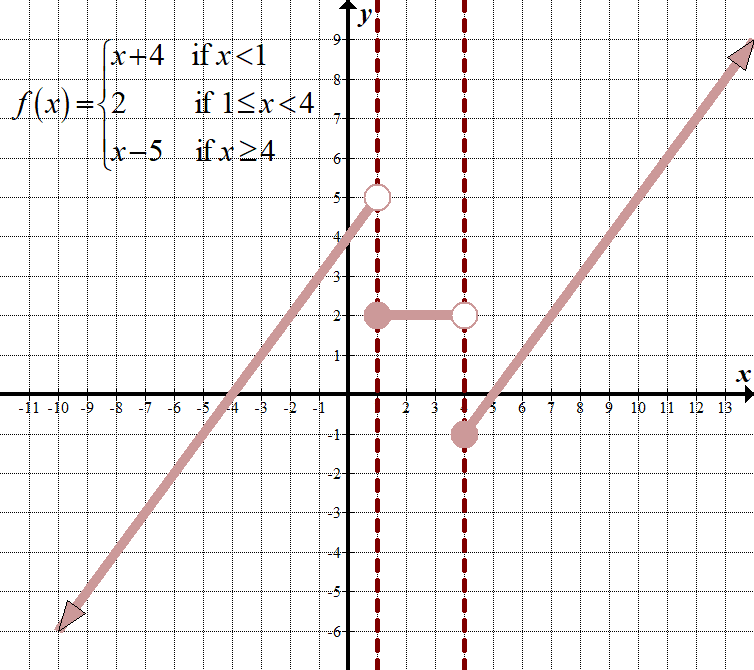We can actually put piecewise functions in the graphing calculator:

Piecewise Function Screens

Steps and Notes

Enter the piecewise function on three lines: Her er grafen:

for at sætte stykkevis funktion \(\displaystyle f\left( h \right)=\left\{ \begynd{array}{L}+4\,\,\,\,\,\,\,\,\,\tekst{hvis} <1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Tekst{Hvis 1} \ le < 4 \ \ -5 + \,\,\,\,\,\ 4\end{array}\højre.\ ) i lommeregneren kan du indtaste funktionen på tre linjer ved at dividere funktionen i hvert interval med en “test ulighed” af dette interval (og se parenteser!). årsagen til, at vi deler med intervaller eller uligheder, er fordi regnemaskinen returnerer en 1, hvis uligheden (som \(<1\)) er sand; for eksempel \((4)\) vil bare ende \((4)/(1)\) når \(<1\). Når \(ge 1\), dividerer vi med 0, så intet vil blive trukket. Her er hvad vi kan lægge i lommeregneren: \(\displaystyle \begin{array}{l}{{Y}_{1}}=\left( {H+4} \right)/\left( {h<1} \right)\\{{Y}_{2}}=\left( 2 \right)/\left( {h\ge 1\tekst{ og}<4} \right)\\{{y}_{3}}=\left( {-5+h} \right)/\left( {h\ge 4} \Right)\end{array}\) (bemærk at du også kan indtaste dette på en linje ved at gange betingelserne i stedet for at dividere og bruge plustegn mellem hver af de tre funktioner/intervaller: \(\displaystyle {{Y}_{1}}=\left( {H+4} \right)\left( {h<1} \right)+\left( 2 \right)\left( {h\ge 1\Tekst{ and }H<4} \right)+\left( {-5+h} \right)\left (4}\højre)\).) Her er tastetryk for at bruge tre linjer. Bemærk, at du bruger 2.Matematik (TEST) for at komme til skærmen, der har \(\le\), \(\ge\) osv. For eksempel får 2. Matematik 6 dig \(\le \). Brug 2. Matematik (TEST), ret til logik, derefter 1, for “og” i \({{Y}_{2}}\).

Sådan fortæller du, om stykkevis funktion er kontinuerlig eller ikke-kontinuerlig

for at fortælle, om en stykkevis graf er kontinuerlig eller ikke-kontinuerlig, Du kan se på grænsepunkterne og se om \(Y\) punktet er det samme på hver af dem. (Hvis \(y\) ‘ s var forskellige, ville der være et “spring” i grafen!)

lad os prøve dette for de funktioner, vi brugte ovenfor:

Piecewise Function	Check Boundary Points
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\)	Let’s check \(x=4\) in both parts of the function, since 4 is the “boundary point”: \(\begin{array}{l}-2(4)+8=0\\\,\,\,\frac{1}{2}(4)-2=0\end{array}\) siden \(0=0\) er denne stykkevis funktion kontinuerlig.
\(\displaystyle f \ left (\right)= \ left \ {\begin{array}{l}+4\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{hvis} <1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Tekst{Hvis 1} \ le < 4 \ \ -5 + \,\,\,\,\,\,\,\,\,\ 4\end{array}\højre.\)	lad os tjekke de to første dele af funktionen. Bemærk i anden del, \(y\) er altid 2: \(\begin{array}{l}1+4=5\\\,\,\,\,\,\,\,\,\,2=2\end{array}\) siden \(5\ne 2\) kan vi stoppe her og bemærke, at denne stykkevis funktion ikke er kontinuerlig. Hvis \(y\) ‘ s var lige, skulle vi gå en for at kontrollere det næste grænsepunkt på \(4\).

indhentning af ligninger fra stykkevis funktion grafer

Du kan blive bedt om at skrive en stykkevis funktion, givet en graf. Nu hvor vi ved, hvad stykkevis funktioner handler om, er det ikke så slemt!

for at gennemgå, hvordan man får ligninger fra lineære grafer, se opnåelse af ligningerne for en linje, og fra kvadratik, Se finde en kvadratisk ligning fra punkter eller en graf.

Her er graferne, med forklaringer på, hvordan man udlede deres stykkevis ligninger:

Piecewise Function Graph	Procedure to get Function
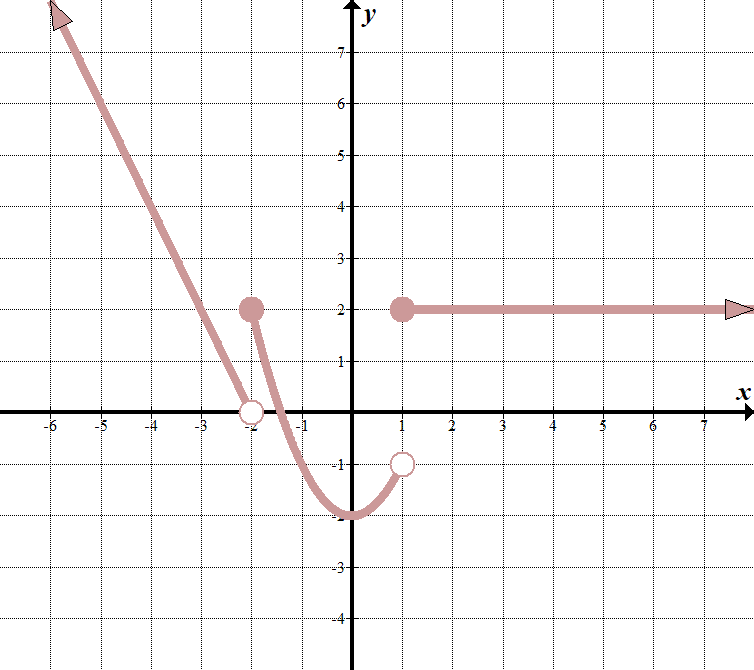	We see that our “boundary lines” are at \(x=-2\) and \(x=1\). We know that our function will look something like this (notice open and closed endpoints): \(\displaystyle f \ left (h \right)= \ left\ {\begin{array}{l}\tekst{ }……\,\,\,\,\,\,\,\,\tekst{hvis } < -2 \ \ \ tekst{ }……\,\,\,\,\,\,\,\,\tekst{if} – \ tekst{2} \ le < 1 \ \ \ tekst{ }……\,\,\,\,\,\,\,\,\tekst{if}\ge 1\end{array} \højre.\) Vi kan vælge to punkter \((-2,0)\) og \((-3,2)\) på venstre linje for at få ligningen \(y=-2h-4\). den midterste funktion er \(y={{}^{2}}-2\), og funktionen længst til højre er kun den vandrette linje \(y=2\). således er den stykkevis funktion: \(\displaystyle f \ left (h \right)=\left\{ \begin{array}{l}-2-4\,\,\,\,\,\,\,\tekst{hvis } < -2 \ \ \ tekst{ }{{}^{2}}-2\,\,\,\,\,\,\,\,\,\,\tekst{if} – \ tekst{2} \ le < 1 \ \ \ tekst{ 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{if}\ge 1\end{array} \højre.\)
	vi ser, at vores “grænselinje” er på \(H=5\). Da linjerne mødes ved \((5,4)\), betyder det ikke noget, hvor vi sætter \(\le\) eller \(\ge\) tegnet; vi kan bare ikke sætte det begge steder, eller det ville ikke være en funktion. Vi har hidtil: \(\displaystyle f \ left (h \right)= \ left \ {\begin{array}{l} \ tekst{ }……\,\,\,\,\,\,\,\,\,\tekst{if } < 5 \ \ \ tekst{ }……\,\,\,\,\,\,\,\,\,\tekst{if}\ge 5\end{array} \højre.\) igen skal vi se på hver linje separat for at bestemme deres ligninger. Vi kan enten tage 2 point fra hver linje for at få disse, eller stamme fra skråninger og \(y\) – aflytninger; stykkevis funktion er: \(\displaystyle f \ left (h \right)= \ left\ {\begin{array}{l} \ frac{6}{5}H-2\,\,\,\,\,\,\,\tekst{if} < 5 \ \ \ frac{2}{5}+2\,\,\,\,\,\,\,\tekst{if}\ge 5\end{array} \højre.\)

absolut værdi som stykkevis funktion

Vi kan skrive absolutte værdifunktioner som stykkevis funktioner – det er virkelig sejt! Du vil måske gennemgå løsning af absolutte værdi Ligninger og uligheder, før du fortsætter videre til dette emne.lad os sige, at vi har funktionen \(f\left( h \right)=\left| h \right|\). Fra det, vi lærte tidligere, ved vi, at når \(S\) er positiv, da vi tager den absolutte værdi, vil det stadig bare være \(s\). Men når \ er negativ, når vi tager den absolutte værdi, er vi nødt til at tage det modsatte (negere det), da den absolutte værdi skal være positiv. Giver mening? Så hvis vi for eksempel havde \(|5|\), tager vi bare det, der er inde i det absolutte tegn, da det er positivt. Men for \(/-5/\) skal vi tage det modsatte (negative) af hvad der er inde i den absolutte værdi for at gøre det \(\displaystyle 5\,\,\,(-\,-5=5)\).

dette betyder, at vi kan skrive denne absolutte værdifunktion som en stykkevis funktion. Bemærk, at vi kan få “vendepunktet” eller “grænsepunktet” ved at indstille det, der er inden for den absolutte værdi, til 0. Så bruger vi enten den oprindelige funktion eller negerer funktionen afhængigt af funktionens tegn (uden den absolutte værdi) i dette interval.

for eksempel kan vi skrive \(\displaystyle \ left|h\right / \ tekst { } = \ left\ {\begin{array}{l}\,\,\,\,\,\,\,\,\,\tekst{if }n\ge 0\ \ -n\,\,\,\,\,\tekst{hvis } <0\end{array} \højre.\). Bemærk også, at hvis funktionen er kontinuerlig (der ikke er noget “spring”) ved grænsepunktet, betyder det ikke noget, hvor vi lægger “mindre end eller lig med” (eller “større end eller lig med”) tegn, så længe vi ikke gentager dem! Vi kan ikke gentage dem, fordi vi teoretisk set ikke kan have to værdier af \(y\) for den samme \(H\), eller vi ville ikke have en funktion.

Here are more examples, with explanations. (You might want to review Quadratic Inequalities for the second example below):

Absolute Value Function	Method to get Piecewise Function
\(g\left( x \right)=\left| {2x+3} \right|\)	Let’s first find the “boundary line”. Vi gør dette ved at indstille, hvad der er inde i den absolutte værdi til 0, og derefter løse for \(\boldsymbol {\}\). Når \(2 gange + 3 \ ge 0\), får vi \(\displaystyle \ ge – \ frac{3}{2}\) (faktisk kan vi beholde \(\ge\) når vi løser). Når \(2 gange + 3\) er positiv, tager vi det bare “som det er”, men hvis det er negativt, skal vi negere det hele. derfor er den stykkevis funktion: \(\displaystyle \ left / {2h + 3} \ right / = \ left\ {\begin{array}{l}2H+3\,\,\,\,\,\,\,\,\,\tekst{if } \ ge- \ frac{3}{2} \ tekst { } \\ – 2-3\,\,\,\,\,\tekst{if } <-\frac{3}{2}\end{array} \højre.\) prøv det – det virker!
\(f\left( h \right)=\left| {{{H}^{2}}-4} \right|\)	lad os først finde” boundary line(s)”; vi sætter hvad der er inde i den absolutte værdi til 0. Når \({{}^{2}}-4 \ ge 0\), får vi \(\le -2\) eller \(\ge 2\) (Prøv nogle tal!). Når \({{}^{2}}-4\) er positiv, tager vi det bare “som det er”, men hvis det er negativt, skal vi negere det. stykkevis funktion er: \(\displaystyle \left / {{{{}^{2}}-4} \ right / = \ left \ {\begin{array}{l}{{}^{2}}-4\,\,\,\,\,\tekst{Hvis }s \ le -2 \ \ 4 – {{s}^{2}}\,\,\,\,\,\tekst{if }-2 << 2 \ \ {{s}^{2}}-4\,\,\,\,\,\2\tekst {}\end {array }\højre.\ ) eller \(\displaystyle \ left / {{{s}^{2}}-4} \ right / =\left\ {\begin{array}{l}{{S}^{2}}-4\,\,\,\,\,\,\tekst{if }s \ le -2 \ tekst { }\,\, \ tekst{eller}\,\, \ tekst{ }s \ ge 2 \ \ 4 – {{s}^{2}}\,\,\,\,\,\,\,\tekst{if }-2 <<2\end{array} \right.\) igen (da funktionen er kontinuerlig), betyder det virkelig ikke noget, hvor vi har \(\le\) og \(\ge\) (i modsætning til \(<\) og \(>\)), så længe vi ikke gentager dem.
\(f\left( h \right)=2 gange+\left| {H+2} \right|\)	denne er lidt vanskeligere, da vi har en \(H\) inden for og uden for den absolutte værdi. For “grænselinjen” bruger vi kun det, der er inde i den absolutte værdi. Når \(2 \ ge 0\), får vi \(ge -2\). Men for stykkevis funktion, vi er nødt til at bruge hele funktionen, herunder den del, der er uden for den absolutte værdi. Så den stykkevis funktion er: \(\displaystyle 2 gange + \left / {2} \ right / = \ left\ {\begin{array}{l}2 gange + +2\,\,\,\,\,\ tekst{if }s \ ge -2 \ \ 2s-s-2\,\,\,\,\,\tekst{if } <-2\end{array} \right.\) lad os forenkle: \(\displaystyle 2 gange + \left / {2} \ right / =\left\ {\begin{array}{l}3 gange+2\,\,\,\,\,\,\,\Tekst{Hvis }s \ ge -2\ \ s-2\,\,\,\,\,\,\,\,\,\,\tekst{if } <-2\end{array} \right.\ ) prøv nogle værdier mindre end og stor derefter -2; de skal arbejde!
\(g\left( h \right)=\left| {{{H}^{2}}-4h-5} \right|\)	denne løses bedst med et tegndiagram, da vi har en kvadratisk, og vi er nødt til at vide, hvor funktionen er positiv og negativ. først faktor kvadratisk inde i funktionen absolut værdi til \(\left ({h-5}\right) \left ({H+1}\right)\). Brug derefter et tegndiagram for at se, hvor faktorerne er positive og negative, og husk, at hvor faktorerne er positive, bruger vi funktionen “som den er”, og hvor faktorerne er negative, negerer vi funktionen: \(\displaystyle \left / {{{{}^{2}} – 4h-5} \ right / = \ left\ {\begin{array}{l} {{{{}}^{2}} – 4h-5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{if } \ le -1\,\,\,\,\tekst{eller}\,\,\,\, \ ge 5 \ \ – \ venstre ({{{}^{2}}-4h-5} \højre)\,\,\,\,\tekst{if }-1 <<5\tekst{ }\end{array} \højre.\)
\(\displaystyle g\left( h \right)=\frac{{\left| {H+2} \right|}}{{H+2}}\)	dette er en rationel funktion, da der er en variabel i nævneren. Når \(2 \ ge 0\), får vi \(\displaystyle \ ge -2\). Når \(H+2\) er positiv, tager vi det bare “som det er”, men hvis det er negativt, skal vi negere hvad der er i den absolutte værdi: \(\displaystyle \frac {{\left / {H + 2} \ right/}} {{H+2}}=\left\{ \begin{array} {l}\frac{{H+2}} {{{H + 2}} = \ left \ {\begin {array} {l} \ frac {{H + 2}} {{{H + 2}}+2}}\,\,\,\,\,\,\,\,\,\ tekst{if }s \ ge -2 \ \ \ frac {{- s-2}}{{s+2}}\,\,\,\,\,\,\tekst{if } <-2\end{array} \right.\). Men vi skal være forsigtige, da \(n \ ne 2\) (domænebegrænsning: nævneren ville være 0). derfor er den stykkevis funktion: \(\displaystyle \frac {{\left / {H + 2} \ right/}} {{H + 2}}= \ left\ {\begin{array}{l}1\,\,\,\,\,\,\,\,\,\,\tekst{hvis } >-2\\-1\,\,\,\,\,\,\tekst{if } <-2\end{array} \right.\).

Du kan også blive bedt om at tage en absolut værdi graf og skrive den som en stykkevis funktion:

Absolute Value Graph	Method to get Piecewise Function
	We see that our “boundary line” is at \(x=0\), so what’s inside the absolute value sign must be \(x\) or a factor of \(x\). (Dette skyldes, at for at få grænselinjen med en absolut værdifunktion, indstiller vi, hvad der er inde i den absolutte værdi til 0, og løser for \(H\)). Når \(>0\), kan vi se, at ligningen af linjen er \(y=2H-2\). Når \(<0\) er ligningen \(y=2H-2\). Vi kan skrive dette som en stykkevis funktion: \(\displaystyle f \ left (\right)= \ left \ {\begin{array}{l}2-2\,\,\,\,\,\,\,\tekst{if } > 0\\-2h-2\,\,\,\tekst{if }0\end{array}\højre.\) Vi kan også skrive dette som en transformeret absolut værdifunktion: \(y=2 \ left / h \ right / -2\) eller \(y=\left| {2h} \right|-2\) (da 2 er positiv, kan det være inden for eller uden for \(\left| {\,\,} \right|\)). (Dette giver mening, da når hvad der er inde i \(\left| { \ ,\,} \right|\) er \(> 0\), bruger vi den almindelige funktion \(y=2H-2\), og når hvad der er inde i er \(< 0\), negerer vi den absolutte værdi del for at gøre det \(y=-\left ({2H} \højre)-2\)).
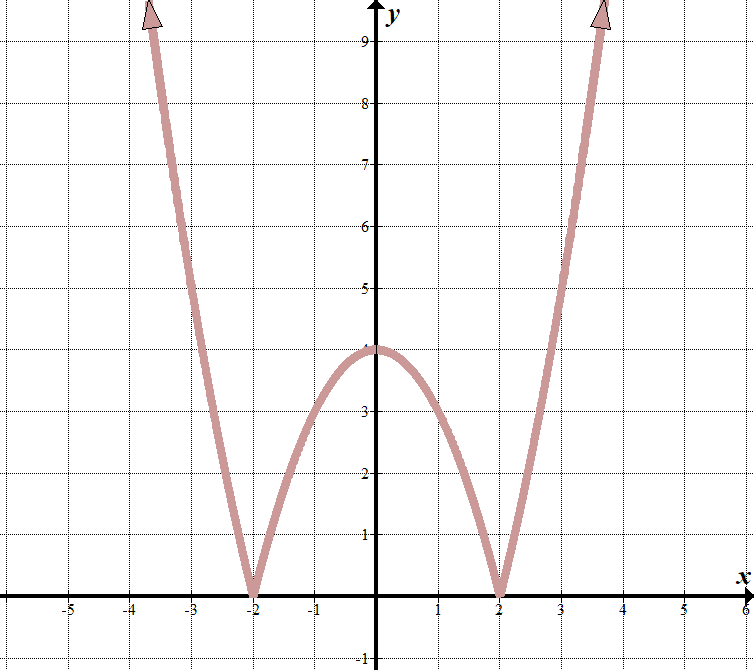	vi ser, at vores “grænselinjer” er på \(H=2\) og \(H=-2\), så hvad er der inde i det absolutte værditegn, skal vi har faktorer af \(H-2\) og \(H+2\). når \(< -2\) eller \(> 2\), kan vi se, at grafen ligner den normale del af grafen \(y={{}^{2}}-4\). (Jeg regnede det ud ved at kende faktorerne og tage et godt gæt!) Når \(-2 <<2\), er ligningen vendt eller negeret (vendt over \(h\)-aksen). Vi kan skrive dette som en stykkevis funktion: \(\displaystyle f \ left (h \right)= \ left \ {\begin{array}{l}{{}^{2}}-4\,\,\,\,\,\,\,\,\,\tekst{hvis } <-2 \ tekst{ eller } > 2 \ \ – {{{}^{2}} \ tekst{+ 4}\,\,\,\,\,\,\tekst{if }-2 \ le 2 \ end{array} \ højre.\) Vi kan se, at dette startede en transformeret kvadratisk funktion \(y={{{}^{2}}-4\) med en absolut værdi omkring den, da alle \(y\) værdier er positive: \(y=\left| {{{{}^{2}}-4} \right|\).
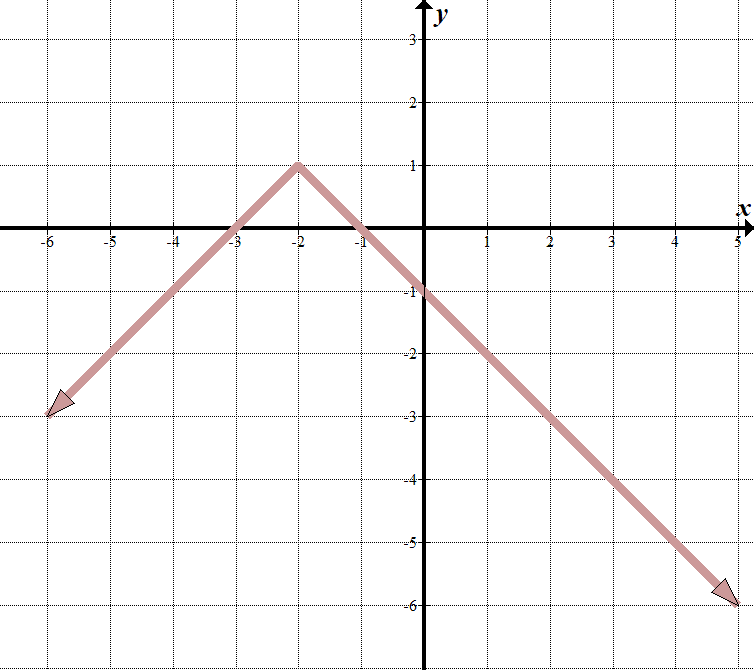	vi ser, at vores “grænselinje” er på \(h=-2\), så hvad der er inde i det absolutte værditegn skal være \(H + 2\). Når \(>-2\), kan vi se, at ligningen af linjen er \(y=-H-1\). Når \(<-2\), er linjen \(y=+3\). Vi kan skrive dette som en stykkevis funktion: \(\displaystyle f \ left (h \right)=\left\{ \begin{array}{l}–1\,\,\,\,\,\,\tekst{if } > -2 \ \ +3\,\,\,\,\,\,\,\,\,\,\ tekst{hvis } \ le -2 \ end{array} \ højre.\) det er nok lettere at skrive dette som en transformeret absolut værdi funktion. Vi kan se, at den overordnede absolutte værdi funktion er vendt lodret, flytte til venstre 2 og op 1. Vores absolutte værdi ligning er \(y= – \ left / {H + 2} \ right|\,\,+\,\,1\). Dette er det samme som den stykkevis funktion ovenfor. Prøv det – det virker!

transformationer af stykkevis funktioner

lad os lave en transformation af en stykkevis funktion. Vi lærte hvad med overordnede funktioner og deres transformationer her i afsnittet overordnede grafer og transformationer. Du vil sandsynligvis gerne læse dette afsnit først, før du prøver en stykkevis transformation.

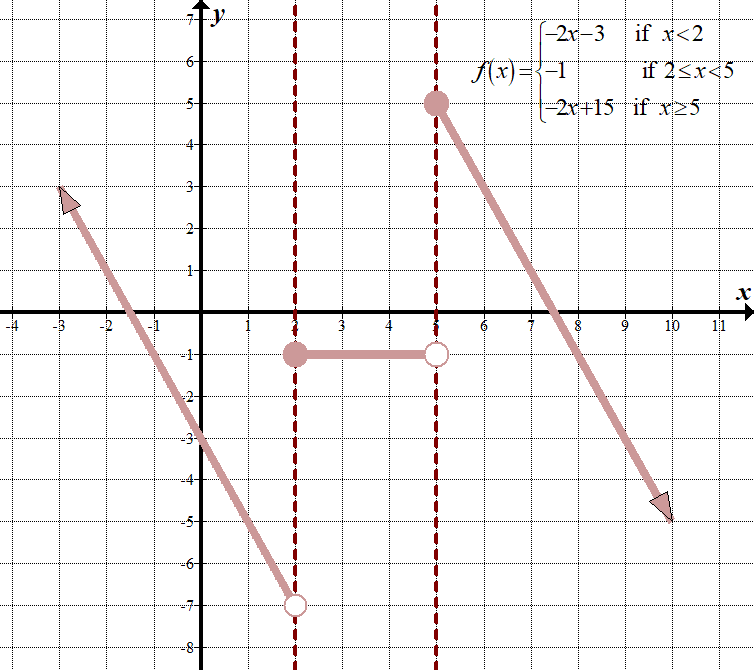
lad os omdanne følgende stykkevis funktion vendt rundt om aksen, lodret strakt med en faktor på 2 enheder, 1 enhed til højre og 3 enheder op.

vi tegner \(- 2F \left( H-1 \ right) + 3\), hvor:

\(\displaystyle f \ left (h \right)= \ left\ {\begin{align}+4\,\,\,\,\,\,\,\,&\tekst{ hvis } <&\tekst{ if 1 } \ le < 4 \ \ H-5\,\,\,\,\,\,\,\,&\tekst{ hvis}\ge 4\end{juster} \højre.\)

lad os sørge for, at vi bruger “grænse”-punkterne, når vi udfylder t-diagrammet til transformationen. Husk, at transformationerne inden for parenteserne er gjort til \(H\) (gør det modsatte matematik), og udenfor er gjort til \(y\). For at komme med et t-diagram, som vist i nedenstående tabel, kan vi bruge nøglepunkter, herunder to punkter på hver af “grænselinjerne”.

Bemærk, at fordi denne transformation er kompliceret, kan vi komme med en ny stykkevis funktion ved at transformere de 3 “stykker” og også transformere “\(h\)”S, hvor grænsepunkterne er (tilføje 1 eller gå til højre 1), Da vi gør det modsatte matematik for “\(H\)”s. For at få de nye funktioner i hvert interval kan vi bare erstatte ” \(1\) “for” \(h\) ” i den oprindelige ligning, multiplicere med -2 og derefter tilføje 3. For eksempel \(\displaystyle-2F\left( {H-1} \right)+3=-2\left+3=-2\left( {H+3} \right)+3=-2h-3\).

\(\displaystyle-2F \ left ({H-1} \ right)+3= \ left\ {\begin{array}{l}-2\left ({\left( {H-1} \right)+4} \ right)+3= – 2-3,\,\,\,\,\tekst{ if }H-1 < 1\,\,\,\venstre ({< 2} \ højre)\ \ -2 \ venstre (2 \ højre)+3=-1,\,\,\,\,\tekst{ if}\, \ tekst{ 2 }\le< 5 \ \-2 \ left ({\left ({1} \right)-5} \right)+3= – 2+15,\,\,\,\,\tekst{ if}\ge 5\end{array} \højre.\)

Her er graferne” før “og” efter”, herunder t-diagrammet:

Piecewise Parent Function	T-chart	Transformation of Function
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\)	x + 1 x y –2y+3 1 0 4 –5 2 1 5 –7 2 1 2 –1 5 4 2 –1 5 4 –1 5 8 7 2 –1	\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2x-3\,\,\,\,\,\,\,\,\,\text{if }x<2\\-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 2}\le x<5\\-2x+15\,\,\,\,\,\,\text{if }x\ge 5\end{array} \right.\)

Piecewise Function Word Problems

Problem:

din favorit hund groomer afgifter i henhold til din hunds vægt. Hvis din hund er 15 pund og under, opkræver groomer $ 35. Hvis din hund er mellem 15 og 40 pund, opkræver hun $40. Hvis din hund er over 40 pund, opkræver hun $40 plus en ekstra $2 for hvert pund.

(a) Skriv en stykkevis funktion, der beskriver, hvad din hund groomer afgifter.

(b) graf funktionen.

(c) Hvad ville groomer opkræve, hvis din søde hund vejer 60 pund?

opløsning:

(A) Vi ser, at “grænsepunkterne” er 15 og 40, da disse er de vægte, hvor priserne ændres. Da vi har to grænsepunkter, har vi tre ligninger i vores stykkevis funktion. Vi er nødt til at starte kl 0, da hunde skal veje over 0 Pund:

\(\displaystyle f \ left (h \right)= \ left \ {\begin{array}{l}\tekst{ }……\,\,\,\,\,\,\,\,\,\tekst{if }0 <h\le 15 \ \ \ tekst{ }……\,\,\,\,\,\,\,\,\,\tekst{if }15 <h\le 40 \ \ \ tekst{ }……\,\,\,\,\,\,\,\,\,\tekst{if } > 40 \end{array} \ højre.\)

Vi leder efter “svarene” (hvor meget plejeomkostningerne) til “spørgsmålene” (hvor meget hunden vejer) for de tre prisintervaller. De to første er bare faste gebyrer (henholdsvis$35 og $40). Den sidste ligning er lidt vanskeligere; groomer opkræver $40 plus $2 for hvert pund over 40. Lad os prøve reelle tal: hvis din hund vejer 60 pund, opkræver hun $40 plus $2 gange \(20(60-40)\). Vi gør dette til en ligning: \(40 + 2 (H–40)\), hvilket forenkler til \(2h–40\) (se hvordan 2 er hældningen?).

hele stykkevis funktion er:

\(\displaystyle f \ left (h \right)= \ left \ {\begin{array}{l}\tekst{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{if }0 <h\le 15 \ \ \ tekst{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{if }15 <h\le 40 \ \ \ tekst{ }40 + 2 \ venstre ({h-40} \ højre)\,\,\,\,\,\,\tekst{if } > 40 \end{array} \ højre.\ ) eller \(\displaystyle f\left (\right)= \ left\ {\begin{array}{l} \ tekst{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{if }0 <h\le 15 \ \ \ tekst{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{if }15 <s\le 40 \ \ \ tekst{ }2s-40\,\,\,\,\,\,\,\tekst{if } > 40 \end{array} \ højre.\)

(b) Lad os graf:Bemærk, at denne stykkevis ligning er ikke-kontinuerlig. Bemærk også, at et rimeligt domæne for dette problem kan være \(\left ({0,200} \right]\) (givne hunde vejer ikke over 200 pund!) og et rimeligt interval kan være \(\left \ cup\left\).

(c) hvis din hund vejer 60 pund, kan vi enten bruge grafen eller funktionen til at se, at du skal betale $80. Hov! Det koster mere end et menneskeligt hårklipp (i det mindste mine hårklipp)!

Problem:

du planlægger at sælge hun elsker matematik T-shirts som en fundraiser. Engros-T-shirt-firmaet opkræver dig $10 en skjorte til de første 75 skjorter. Efter de første 75 skjorter, du køber op til 150 skjorter, vil virksomheden sænke prisen til $7,50 pr. Når du har købt 150 skjorter, vil prisen falde til $5 pr. Skriv en funktion, der modellerer denne situation.

løsning:

Vi ser, at “grænsepunkterne” er 75 og 150, da dette er antallet af købte T-shirts, hvor priserne ændres. Da vi har to grænsepunkter, har vi tre ligninger i vores stykkevis funktion. Vi starter med \(GE 1\), Da vi antager, at mindst en skjorte er købt. Bemærk i dette problem skal antallet af købte T-shirts eller domænet være et heltal, men denne begrænsning bør ikke påvirke udfaldet af problemet.

\(\displaystyle f\left( h \right)=\left\{ \begin{array}{l}\tekst{ }……\tekst{ if }1\le h\le 75\\\tekst{ }……\tekst{ if }75<h\le 150\\\tekst{ }……\tekst{ hvis}>150\end{array} \højre.\)

vi leder efter “svarene” (samlede omkostninger ved t-shirts) til “spørgsmålene” (Hvor mange er købt) for de tre prisklasser.

for op til og med 75 skjorter er prisen $10, så den samlede pris ville \(10 gange\). For mere end 75 skjorter, men op til 100 skjorter, er prisen $7,50, men de første 75 t-shirts koster stadig $10 pr. Den anden funktion inkluderer $750 brugt på de første 75 skjorter (75 gange $10) og inkluderer også $7,50 gange antallet af skjorter over 75, hvilket ville være \((75)\). For eksempel, hvis du har købt 80 skjorter, skal du bruge \(\$10 \ gange 75=\$750\) plus \(\$7,50 \ gange 5\,\) (80 – 75) til skjorterne efter den 75.skjorte.

tilsvarende vil vi for over 150 skjorter stadig betale $10-prisen op gennem 75 skjorter, $7.50 pris for 76 til 150 skjorter (75 flere skjorter), og derefter $5 per skjorte for antallet af skjorter købt over 150. Vi betaler \(10(75)+7.50(75)+5(150)\) til skjorter. Sæt i tal og prøv det!

hele stykkevis funktion er:

\(\displaystyle f \ left (h \right)= \ left \ {\begin{array}{l} \ tekst{ }10\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{if }1 \ le 75 \ \ \ tekst{ }7.5 \ Tekst { } + \ Tekst{ }187.5\,\,\,\,\,\tekst{Hvis 7}5<150\\\tekst{ }5 gange+562.5\,\,\,\,\,\,\,\,\,\,\tekst{ if } > 150 \end{array} \ højre.\ ) eller \(\displaystyle f\left( h \right)= \ left\ {\begin{array}{l} \ tekst{ }10\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\tekst{if }1 \ le 75 \ \ \ tekst{ }7.5 \ Tekst { } + \ Tekst{ }187.5\,\,\,\,\,\tekst{Hvis 7}5 < h \ le 150 \ \ \ tekst{ }5+562.5\,\,\,\,\,\,\,\,\,\,\,\tekst{if } > 150 \end{array} \ højre.\)

Problem:

en busforbindelse koster $50 for de første 400 miles, og hver yderligere 300 miles (eller en brøkdel deraf) tilføjer $10 til billetprisen.

brug en stykkevis funktion til at repræsentere busbilletten med hensyn til afstanden i miles.

løsning:

Dette er faktisk et vanskeligt problem, men lad os først tænke på “grænsepunktet”, som er 400. Det er ret ligetil, når turen er mindre end 400 miles; prisen er $50.

for mere end 400 miles skal vi trække de første 400 miles ud (men husk at inkludere de første $50), divider antallet af miles tilbage med 300 miles (og runde op, hvis der er en brøkdel), og multiplicer det med $10.

den vanskelige del er, når vi “runde op” for en del af de næste 300 miles. Vi kan bruge en “loft” – funktion (betegnet med \(\left\lceil {} \right\rceil \)); denne funktion giver det mindste heltal, der er større end eller lig med dets input; for eksempel er loftet på både 3,5 og 4 4.

således er det, hvad vi har:

\(\displaystyle f \ left (h \right)= \ left\ {\begin{array}{l} \ tekst{ }50 \ tekst{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Tekst{Hvis }0 \ le 400 \ \ \ Tekst{ }50+10 \ gange \left\lceil {\frac{{-400}}{{300}}} \højre\rceil \ tekst{ }\,\,\,\,\,\,\tekst{ if } > 400 \end{array} \ højre.\)

lad os prøve det! Hvis vi har en 1500-mile tur, ville omkostningerne være \(\displaystyle 50+10 \ times \ left \ lceil {\frac{{1500-400}}{{300}}} \højre\rceil \ tekst{ }=50 + 10\gange 4=\$90\).

Problem:

hvilken værdi af \(\boldsymbol{a}\) ville gøre denne stykkevis funktion kontinuerlig?

\(\displaystyle f \ left (h \right)= \ left \ {\begin{array}{l} 3{{H}^{2}}+4\,\,\,\,\,\tekst{ if } <-2 \ \ 5 gange+ \ boldsymbol{a}\,\,\,\,\,\,\,\,\tekst{if}\ge -2\end{array} \højre.\)

løsning:

for at den stykkevis funktion skal være kontinuerlig, ved grænsepunktet (hvor funktionen ændres), skal de to \(y\) værdier være de samme. Vi kan tilslutte -2 til \(H\) I begge funktioner og sørge for, at \(y\)’erne er de samme

\(\begin{align}3{{H}^{2}}+4& =5 gange+a\\3 {{\left ({-2} \ right)}^{2}}+4&=5\left( {-2} \right)+a\\12+4&=-10+a\\a&=26\end{align}\)

Hvis \(A=26\), er stykkevis funktion kontinuerlig!

Lær disse regler,og praksis, praksis, praksis!

mere øvelse: brug Matematikkontrollen nedenfor for at prøve at skrive en stykkevis funktion. Klik på Send (den blå pil til højre for problemet) og klik på Skriv den absolutte værdi som stykkevis for at se svaret.

Du kan også indtaste dit eget problem eller klikke på de tre prikker i øverste højre hjørne og klikke på “eksempler” for at bore ned efter emne.

Hvis du klikker på tryk for at se trin, eller klik her, kan du tilmelde dig en gratis prøveperiode og derefter opgradere til et betalt abonnement til enhver tid (for at få enhver form for matematikproblem løst!).

videre til matricer og løse systemer med matricer – du er klar!