Konigsberg er en by ved Preger-floden, som i det 18.århundredevar en tysk by, men nu er russisk. Inden for byen er toflodøer, der er forbundet med bankerne med syv broer(som vist nedenfor).

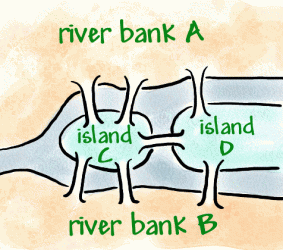
det blev en tradition at forsøge at gå rundt i byen på en måde, somkun krydsede hver bro en gang, men det viste sig at være et sværtproblem. Leonhard Euler, en svensk matematiker i tjenesten afDen Russiske kejserinde Katarina den store, hørte om problemet.I 1736 Euler bevist, at turen ikke var muligt at gøre. Hanbeviste dette ved at opfinde en slags diagram kaldet et netværk, detbestår af hjørner (prikker hvor linjer mødes) og buer(linjer).

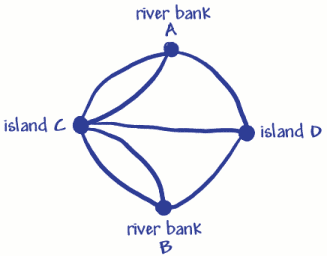
han brugte fire prikker (hjørner) til de to flodbredder og de to øer. Disse er markeret A, B og C, D. De syv linjer(buer) er de syv broer. Du kan se, at 3 broer (buer)slutter sig til flodbredden A, og 3 slutter sig til flodbredden B. 5 broer (buer)slutter sig til øen C, og 3 slutter sig til øen D. Det betyder, at allevertices har et ulige antal buer, så de kaldes oddvertices. (Et jævnt toppunkt skulle have et lige antal buertilsluttende sig til det).
Husk, at problemet var at rejse rundt i byen krydser everybridge kun en gang. På Eulers netværk betød dette kun at spore over everyarc en gang og besøge alle hjørnerne. Euler beviste, at det ikke kunne gøres, fordi han udarbejdede, at for at have et underligt toppunkt, ville du begynde eller afslutte turen ved det toppunkt. (Tænk over det).Da der kun kan være en begyndelse og en ende, kan der kun være to ulige hjørner, hvis du kun kan spore over eacharc en gang. Da broproblemet har 4 ulige hjørner, er det ikke muligt at gøre! Hvad sker der, hvis der ikke er ulige hjørner påalt? Kan dette netværk spores?

opfindelsen af netværk begyndte en helt ny type geometri kaldettopologi. Topologi bruges nu på mange måder, herunder til planlægningog kortlægning af jernbanenet. (Ahhh! Tog måtte komme indDet….)