- læringsmål
- arbejde udført mod tyngdekraften
- konvertering mellem potentiel energi og kinetisk energi
- brug af potentiel energi til at forenkle beregningerne
- eksempel 1. Kraften til at stoppe med at falde
- strategi
- opløsning
- Diskussion
- eksempel 2. Find hastigheden på en rutsjebane fra dens højde
- strategi
- opløsning til Del 1
- løsning til del 2
- diskussion og implikationer
- oprettelse af forbindelser: Take-Home Investigation—konvertering af potentiale til kinetisk energi
- Sektionsoversigt
- konceptuelle spørgsmål
- problemer& øvelser
- ordliste
- udvalgte løsninger på problemer& øvelser
læringsmål
ved udgangen af dette afsnit vil du være i stand til at:
- forklare gravitationel potentiel energi med hensyn til arbejde udført mod tyngdekraften.
- viser, at gravitationspotentialenergien af et objekt med masse m i højden h på jorden er givet af PEg = mgh.
- Vis, hvordan viden om den potentielle energi som funktion af position kan bruges til at forenkle beregninger og forklare fysiske fænomener.
arbejde udført mod tyngdekraften
klatring af trapper og løfteobjekter er arbejde i både videnskabelig og dagligdags forstand—det er arbejde udført mod tyngdekraften. Når der er arbejde, er der en transformation af energi. Arbejdet mod tyngdekraften går ind i en vigtig form for lagret energi, som vi vil udforske i dette afsnit.

Figur 1. (A) det arbejde, der udføres for at løfte vægten, lagres i masse-jord-systemet som gravitationspotentiel energi. (b) når vægten bevæger sig nedad, overføres denne tyngdepotentielle energi til gøguret.
lad os beregne det arbejde, der udføres ved at løfte et objekt med masse m gennem en højde h, som i Figur 1. Hvis genstanden løftes lige op med konstant hastighed, er den kraft, der er nødvendig for at løfte den, lig med dens vægt mg. Arbejdet på massen er derefter V = Fd = mgh. Vi definerer dette som den gravitationelle potentielle energi (PEg), der er sat i (eller opnået af) objekt-jord-systemet. Denne energi er forbundet med tilstanden af adskillelse mellem to objekter, der tiltrækker hinanden af tyngdekraften. For nemheds skyld henviser vi til dette som PEg opnået af objektet, idet vi erkender, at dette er energi lagret i Jordens tyngdefelt. Hvorfor bruger vi ordet “system”? Potentiel energi er en egenskab af et system snarere end af et enkelt objekt—på grund af dets fysiske position. Et objekts tyngdepotentiale skyldes dets position i forhold til omgivelserne i Jordobjektsystemet. Den kraft, der påføres objektet, er en ekstern kraft uden for systemet. Når det gør positivt arbejde, øger det systemets gravitationspotentielle energi. Fordi gravitationspotentiel energi afhænger af relativ position, har vi brug for et referenceniveau, hvor den potentielle energi skal indstilles til 0. Vi vælger normalt dette punkt til at være jordens overflade, men dette punkt er vilkårligt; hvad der er vigtigt er forskellen i gravitationel potentiel energi, fordi denne forskel er, hvad der vedrører det udførte arbejde. Forskellen i gravitationspotentialenergi for et objekt (i Jordobjektsystemet) mellem to trin på en stige vil være den samme for de to første trin som for de sidste to trin.
konvertering mellem potentiel energi og kinetisk energi
gravitationel potentiel energi kan omdannes til andre former for energi, såsom kinetisk energi. Hvis vi frigiver massen, vil tyngdekraften udføre en mængde arbejde svarende til mgh på den og derved øge dens kinetiske energi med den samme mængde (ved arbejdsenergi-sætningen). Vi vil finde det mere nyttigt at overveje kun konverteringen af PEg til KE uden eksplicit at overveje det mellemliggende trin i arbejdet. (Se Eksempel 2.) Denne genvej gør det lettere at løse problemer ved hjælp af energi (hvis muligt) snarere end eksplicit at bruge kræfter.
mere præcist definerer vi ændringen i gravitationspotentialenergien Rog peg til at være Rog peg = mgh, hvor vi for enkelhedens skyld angiver ændringen i højden med h snarere end den sædvanlige Rog. Bemærk, at h er positiv, når den endelige højde er større end den oprindelige højde, og omvendt. For eksempel, hvis en 0,500 kg masse hængt fra et gøgur hæves 1.00 m, så er dens ændring i gravitationel potentiel energi
\begin{array}{lll}mgh&&(0,500\tekst{ kg})(9,80\tekst{ m/s}^2)(1.00\tekst{ m})\\\tekst {}&&4.90\tekst{ kg}\cdot\tekst{m}^2\Tekst{/s}^2=4.90\tekst{ j}\end{array}\\
bemærk, at enhederne af gravitationel potentiel energi viser sig at være joules, det samme som for arbejde og andre former for energi. Når uret kører, sænkes massen. Vi kan tænke på massen som gradvist at opgive sin 4.90 J af gravitationspotentiel energi uden direkte at overveje tyngdekraften, der udfører arbejdet.
brug af potentiel energi til at forenkle beregningerne

figur 2. Ændringen i gravitationspotentialenergi (Krupeg) mellem punkterne A og B er uafhængig af stien.
ligningen Prispeg = mgh gælder for enhver sti, der har en ændring i højden på h, ikke kun når massen løftes lige op. (Se Figur 2.) Det er meget lettere at beregne mgh (en simpel multiplikation) end det er at beregne det arbejde, der udføres langs en kompliceret sti. Ideen om gravitationel potentiel energi har den dobbelte fordel, at den er meget bredt anvendelig, og det gør beregningerne lettere.
fra nu af vil vi overveje, at enhver ændring i lodret position h af en masse m ledsages af en ændring i gravitationel potentiel energi mgh, og vi vil undgå den tilsvarende, men vanskeligere opgave at beregne arbejde udført af eller mod tyngdekraften.
Prispeg = mgh for enhver sti mellem de to punkter. Tyngdekraften er en af en lille klasse af kræfter, hvor arbejdet udført af eller mod kraften kun afhænger af start-og slutpunkterne, ikke på stien mellem dem.
eksempel 1. Kraften til at stoppe med at falde
a 60.0-kg person hopper på gulvet fra en højde på 3,00 m. hvis han lander stift (med knæledene komprimeres med 0,500 cm), skal du beregne kraften på knæledene.
strategi
denne persons energi bringes til nul i denne situation ved det arbejde, der udføres på ham ved gulvet, når han stopper. Den oprindelige pind omdannes til KE, når han falder. Arbejdet udført af gulvet reducerer denne kinetiske energi til nul.
opløsning
arbejdet udført på personen ved gulvet, når han stopper, er givet af V = Fd cos LARP = −Fd, med et minustegn, fordi forskydningen under stop og kraften fra gulvet er i modsatte retninger (cos LARP = cos 180 LARP = -1). Gulvet fjerner energi fra systemet, så det gør negativt arbejde.
den kinetiske energi, personen har, når han når gulvet, er mængden af potentiel energi, der går tabt ved at falde gennem højden h: KE = −Pripeg = −mgh.
afstanden d, som personens knæ bøjer, er meget mindre end højden h af efteråret, så den yderligere ændring i gravitationspotentialenergi under knæbøjningen ignoreres.
arbejdet med gulvet på personen stopper personen og bringer personens kinetiske energi til nul: V = −KE = mgh.
Ved at kombinere denne ligning med udtrykket for V giver-Fd = mgh.
minder om, at h er negativ, fordi personen faldt ned, kraften på knæleddet er givet af
\displaystyle{F}=-\frac{mgh}{d}=-\frac{\left(60.0\tekst{ kg}\right)\left(9.80\tekst{ m/s}^2\right)\left(-3.00\tekst{ m}\right)}{5.00\times10^{-3}\tekst{ m}}=3.53\times10^5\tekst{ N}\\
Diskussion
en sådan stor kraft (500 gange mere end personens vægt) over den korte slagtid er nok til at knæk knogler. En meget bedre måde at dæmpe chokket på er ved at bøje benene eller rulle på jorden, hvilket øger den tid, hvor kraften virker. En bøjningsbevægelse på 0,5 m på denne måde giver en kraft 100 gange mindre end i eksemplet. En kænguruhopping viser denne metode i aktion. Kænguruen er det eneste store dyr, der bruger hopping til bevægelse, men chokket ved hopping dæmpes ved bøjning af bagbenene i hvert spring. (Se Figur 3.)

figur 3. Arbejdet udført af jorden på kænguruen reducerer sin kinetiske energi til nul, når den lander. Ved at anvende jordens kraft på bagbenene over en længere afstand reduceres påvirkningen på knoglerne. (kredit: Chris Samuel, Flickr)
eksempel 2. Find hastigheden på en rutsjebane fra dens højde
- hvad er den endelige hastighed på rutsjebanen vist i figur 4, hvis den starter fra hvile øverst på 20,0 m bakken, og arbejde udført af friktionskræfter er ubetydelig?
- hvad er dens endelige hastighed (igen under forudsætning af ubetydelig friktion), hvis dens indledende hastighed er 5,00 m/s?
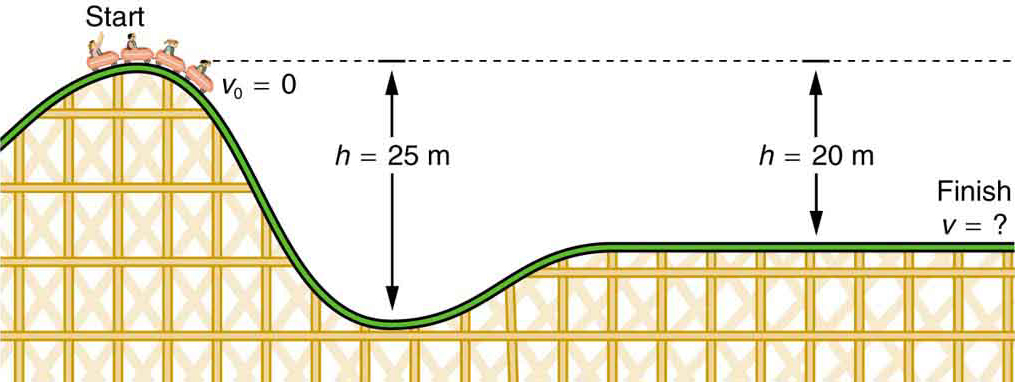
figur 4. Hastigheden på en rutsjebane øges, når tyngdekraften trækker den ned ad bakke og er størst på sit laveste punkt. Set med hensyn til energi omdannes rutsjebane-Jordsystemets tyngdepotentielle energi til kinetisk energi. Hvis arbejde udført ved friktion er ubetydelig, konverteres Al Ryppeg til KE.
strategi
rutsjebanen mister potentiel energi, når den går ned ad bakke. Vi forsømmer friktion, så den resterende kraft, der udøves af sporet, er den normale kraft, som er vinkelret på bevægelsesretningen og ikke fungerer. Nettoarbejdet på rutsjebanen udføres derefter af tyngdekraften alene. Tabet af gravitationspotentiel energi fra at bevæge sig nedad gennem en afstand h svarer til gevinsten i kinetisk energi. Dette kan skrives i ligningsform som-Rrpeg = RRK. Ved hjælp af ligningerne for PEg og KE kan vi løse for den endelige hastighed v, som er den ønskede mængde.
opløsning til Del 1
Her er den oprindelige kinetiske energi nul, så \Delta\tekst{KE}=\frac{1}{2}mv^2\\. Ligningen for ændring i potentiel energi angiver, at Krpeg = mgh. Da h er negativ i dette tilfælde, vil vi omskrive dette som Ryppeg = −mg|h| for at vise minustegnet tydeligt. Således bliver-Reverpeg = reverk mg|h|=\frac{1}{2}{mv}^2\\.
løsning for v finder vi, at massen annullerer, og at v=\kvm{2G|h|}\\.
udskiftning af kendte værdier,
\begin{array}{lll}v&&\kvm{2\venstre(9.80\tekst{ m/s}^2\højre)\venstre(20.0\tekst{ m}\right)}\\\tekst{ }&&19.8\tekst{ m/s}\end{array}\\
løsning til del 2
igen −prispeg = lirke. I dette tilfælde er der indledende kinetisk energi, så
\Delta\tekst{KE}=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\\.
således mg / h / =\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\\.
omarrangering giver \frac{1}{2}mv^2=mg|h / +\frac{1}{2}mv+0^2\\.
dette betyder, at den endelige kinetiske energi er summen af den oprindelige kinetiske energi og gravitationspotentialenergien. Masse igen annullerer, og v= \ KVRT{2G|h / +v_0^2}\\.
denne ligning ligner meget kinematikligningen v = \ KVRT{v_0^2 + 2AD}\\, men den er mere generel—kinematikligningen er kun gyldig for konstant acceleration, mens vores ligning ovenfor er gyldig for enhver sti uanset om objektet bevæger sig med en konstant acceleration. Nu giver erstatning af kendte værdier
\begin{array}{lll}v&&\kvm{2\venstre(9.80\tekst{ m/s}^2\højre)\venstre(20.0\tekst{ m}\højre)+\venstre(5.00\tekst{ m/s}\højre)^2}\\\tekst{ }&&20.4 \ tekst{ m / s} \ end{array}\\
diskussion og implikationer
bemærk først, at massen annullerer. Dette er helt i overensstemmelse med observationer foretaget i faldende genstande, at alle objekter falder i samme hastighed, hvis friktion er ubetydelig. For det andet overvejes kun rutsjebanens hastighed; der er ingen oplysninger om dens retning på noget tidspunkt. Dette afslører en anden generel sandhed. Når friktionen er ubetydelig, afhænger hastigheden af en faldende krop kun af dens indledende hastighed og højde og ikke af dens masse eller den vej, der er taget. For eksempel vil rutsjebanen have den samme endelige hastighed, uanset om den falder 20,0 m lige ned eller tager en mere kompliceret sti som den i figuren. For det tredje og måske uventet er den endelige hastighed i del 2 større end i Del 1, men langt mindre end 5,00 m/s. endelig skal du bemærke, at hastigheden kan findes i enhver højde undervejs ved blot at bruge den passende værdi af h på interessepunktet.
Vi har set, at arbejde udført af eller mod tyngdekraften kun afhænger af start-og slutpunkterne og ikke på stien imellem, hvilket giver os mulighed for at definere det forenklede koncept for gravitationspotentiel energi. Vi kan gøre det samme for et par andre kræfter, og vi vil se, at dette fører til en formel definition af loven om bevarelse af energi.
oprettelse af forbindelser: Take-Home Investigation—konvertering af potentiale til kinetisk energi
man kan studere omdannelsen af gravitationspotentiel energi til kinetisk energi i dette eksperiment. På en glat, plan overflade skal du bruge en lineal af den slags, der har en rille, der løber langs dens længde, og en bog til at gøre en hældning (se figur 5). Placer en marmor i 10 cm-positionen på linealen, og lad den rulle linealen ned. Når det rammer den jævne overflade, måles den tid, det tager at rulle en meter. Placer nu marmoren i positionerne 20 cm og 30 cm, og mål igen de gange, det tager at rulle 1 m på den jævne overflade. Find marmorens hastighed på den jævne overflade for alle tre positioner. Plot hastighed kvadreret versus afstanden tilbagelagt af marmor. Hvad er formen på hvert plot? Hvis formen er en lige linje, viser plottet, at marmorens kinetiske energi i bunden er proportional med dens potentielle energi ved frigivelsespunktet.

figur 5. En marmor ruller ned en lineal, og dens hastighed på den plane overflade måles.
Sektionsoversigt
- arbejde udført mod tyngdekraften ved løft af et objekt bliver potentiel energi i objekt-jordsystemet.
- ændringen i gravitationspotentiel energi, Roppeg, er Roppeg = mgh, hvor h er stigningen i højden og g accelerationen på grund af tyngdekraften.
- gravitationspotentialenergien af et objekt nær jordens overflade skyldes dets position i masse-jord-systemet. Kun forskelle i gravitationel potentiel energi, Krypeg, har fysisk betydning.
- når et objekt falder uden friktion, ændres dets gravitationspotentielle energi til kinetisk energi svarende til stigende hastighed, således at Reykjavik = −Reykjavik
konceptuelle spørgsmål
- I eksempel 2 beregnede vi den endelige hastighed på en rutsjebane, der faldt ned 20 m i højden og havde en starthastighed på 5 m/s ned ad bakke. Antag, at rutsjebanen havde haft en indledende hastighed på 5 m/s op ad bakke i stedet, og den kørte op ad bakke, stoppede og rullede derefter tilbage til et sidste punkt 20 m under starten. Vi ville i så fald finde ud af, at det havde den samme endelige hastighed. Forklar med hensyn til bevarelse af energi.
- afhænger det arbejde, du udfører på en bog, når du løfter den på en hylde, af den vej, du tager? På den tid det tager? På højden af hylden? På bogens masse?
problemer& øvelser
- et vandkraftværk (se figur 6) konverterer vandets tyngdepotentielle energi bag en dæmning til elektrisk energi. (a) Hvad er gravitationspotentialenergien i forhold til generatorerne af en sø med volumen 50.0 km3 (masse = 5,00 kr 1013 kg), da søen har en gennemsnitlig højde på 40,0 m over generatorerne? (B) Sammenlign dette med den energi, der er lagret i en 9-megaton fusionsbombe.

figur 6. (A) hvor meget gravitationspotentiel energi (i forhold til jorden, som den er bygget på) opbevares i Cheops Store Pyramide, da dens masse er omkring 7 til 109 kg og dens massecenter er 36.5 m over den omgivende jord? (b) hvordan er denne energi sammenlignelig med en persons daglige fødeindtagelse?
- Antag, at en 350 g kookaburra (en stor kingfisher-fugl) henter en 75 g slange og hæver den 2,5 m fra jorden til en gren. (A) hvor meget arbejde udførte fuglen på slangen? (b) hvor meget arbejde gjorde den for at rejse sit eget messecenter til grenen?
- i Eksempel 2 fandt vi, at hastigheden på en rutsjebane, der var faldet ned 20,0 m, kun var lidt større, når den havde en starthastighed på 5,00 m/s, end da den startede fra hvile. Dette indebærer, at KRISHPE >> KEi. Bekræft denne erklæring ved at tage forholdet mellem KRP og KEi. (Bemærk, at masse annullerer.)
- en 100 g legetøjsbil drives af en komprimeret fjeder, der starter den i bevægelse. Bilen følger det buede spor i Figur 7. Vis, at legetøjsbilens endelige hastighed er 0,687 m/s, hvis dens indledende hastighed er 2,00 m/s, og den kaster op ad den friktionsløse hældning og får 0,180 m i højden.

Figur 7. En legetøjsbil bevæger sig op ad et skrånende spor. i en alpint ski løb, overraskende, lille fordel opnås ved at få en kørende start. (Dette skyldes, at den oprindelige kinetiske energi er lille sammenlignet med gevinsten i gravitationspotentiel energi på selv små bakker.) For at demonstrere dette skal du finde den endelige hastighed og den tid, det tager for en skiløber, der skyder 70,0 m langs en hældning på 30 liter, der forsømmer friktion: (a) startende fra hvile. (B) Start med en starthastighed på 2,50 m/s. (c) overrasker svaret dig? Diskuter, hvorfor det stadig er fordelagtigt at få en løbende start i meget konkurrencedygtige begivenheder.
ordliste
gravitationspotentiel energi: energien et objekt har på grund af sin position i et tyngdefelt
udvalgte løsninger på problemer& øvelser
1. (a) 1,96-1016 J; (b) forholdet mellem gravitationspotentiel energi i søen og den energi, der er lagret i bomben, er 0,52. Det vil sige, at energien, der er lagret i søen, er cirka halvdelen af den i en 9-megaton fusionsbombe.
3. a) 1.8 J; b) 8.6 j
5. {v}_{f} = \ tekst{2GH + {v_0}^2}=\tekst{2 \ venstre (9.80 \ tekst{ m / s}^2 \ højre) \ venstre (-0.180 \ tekst{ m} \ højre) + \venstre (2.00 \ tekst{ m / s} \ højre)^2}=0.687\tekst{ m/s}\ \