efter at have forstået den eksponentielle funktion er vores næste mål den naturlige logaritme.

i betragtning af hvordan den naturlige log er beskrevet i matematiske bøger, er der lidt “naturligt” om det: det er defineret som det inverse af $e^$, en mærkelig nok eksponent allerede.

men der er en frisk, intuitiv forklaring: den naturlige log giver dig den tid, der er nødvendig for at nå et bestemt vækstniveau.

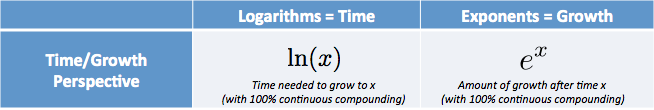
Antag at du har en investering i gummy bears (hvem gør det ikke?) med en rente på 100% om året, vokser kontinuerligt. Hvis du vil have 10 gange vækst, forudsat kontinuerlig sammensætning, vil du kun vente $\ln(10)$ eller 2.302 år. Kan du ikke se, hvorfor det kun tager et par år at få 10 gange vækst? Kan du ikke se, hvorfor mønsteret ikke er 1, 2, 4, 8? Læs mere om e.

e og den naturlige Log er tvillinger:

• $e^$ er det beløb, vi har efter start ved 1.0 og vokser kontinuerligt for$ $ enheder af tid
• $ \ ln ($) $ (naturlig logaritme) er tiden til at nå beløb$$, forudsat at vi voksede kontinuerligt fra 1.0

ikke så dårligt, ikke? Mens matematikerne kæmper for at give dig den lange, tekniske forklaring, lad os dykke ned i den intuitive.

E handler om vækst

tallet e handler om kontinuerlig vækst. Som vi så sidste gang, lader $e^$ os fusionere sats og tid: 3 år ved 100% vækst er den samme som 1 år ved 300% vækst, når den kontinuerligt forværres.

Vi kan tage enhver kombination af sats og tid (50% i 4 år) og konvertere satsen til 100% for nemheds skyld (giver os 100% i 2 år). Ved at konvertere til en hastighed på 100% skal vi kun tænke på tidskomponenten:

intuitivt betyder $e^$:

• hvor meget vækst får jeg efter tidsenheder (og 100% kontinuerlig vækst)
• for eksempel: efter 3 tidsperioder har jeg $e^3$ = 20,08 gange mængden af “ting”.

$e^ $ er en skaleringsfaktor, der viser os, hvor meget vækst vi ville få efter $$ enheder af tid.

naturlig Log er på tide

den naturlige log er den inverse af $e^$, en fancy betegnelse for modsat. Apropos fancy, det latinske navn er logarithmus naturali, hvilket giver forkortelsen ln.

hvad betyder denne omvendte eller modsatte ting?

• $e^$ giver os mulighed for at tilslutte tid og få vækst.$ \ ln$ giver os mulighed for at tilslutte vækst og få den tid, det ville tage.

for eksempel:

• $e^3$ er 20,08. Efter 3 enheder af tid, vi ender med 20.08 gange hvad vi startede med.
• $ \ ln (20.08)$ er omkring 3. Hvis vi ønsker vækst på 20.08, vil vi vente 3 enheder af tid (igen, forudsat en 100% kontinuerlig vækstrate).

med mig? Den naturlige log giver os den nødvendige tid til at ramme vores ønskede vækst.

logaritmisk aritmetik er ikke Normal

du har studeret logfiler før, og de var mærkelige dyr. Hvordan gjorde de multiplikation til tilføjelse? Opdeling i subtraktion? Lad os se.

Hvad er $ \ ln (1)$? Intuitivt er spørgsmålet: Hvor længe venter jeg på at få 1 gang mit nuværende beløb?

nul. Zip. Nada. Du er allerede på 1 gange dit nuværende beløb! Det tager ikke tid at vokse fra 1 til 1.

• $\ln (1) = 0$

Ok, hvad med en brøkdel? Hvor lang tid får jeg 1/2 mit nuværende beløb? Forudsat at du vokser kontinuerligt på 100%, ved vi, at $\ln(2)$ er mængden af tid til at fordoble. Hvis vi vender det (dvs. tager den negative tid), ville vi have halvdelen af vores nuværende værdi.

• $\ln(.5) = – \ ln (2)= -.693$

giver mening, ikke? Hvis vi går baglæns .693 enheder (negative sekunder, lad os sige) vi ville have halvdelen af vores nuværende beløb. Generelt kan du vende fraktionen og tage det negative: $\ln(1/3) = – \ln(3) = -1.09$. Det betyder, at hvis vi går tilbage 1,09 enheder af tid, ville vi have en tredjedel af det, vi har nu.

Ok, hvad med den naturlige log af et negativt tal? Hvor lang tid tager det at “vokse” din bakteriekoloni fra 1 til -3?

det er umuligt! Du kan ikke have en “negativ” mængde bakterier, kan du? Mindst) kan du have nul, men der er ingen måde at have en negativ mængde af de små critters. Negative bakterier giver bare ikke mening.

• $\ln(\tekst{negativt tal}) = \tekst{undefined}$

Undefined betyder bare “der er ingen tid, du kan vente” for at få et negativt beløb. (Nå, hvis vi bruger imaginære eksponentialer, er der en løsning. Men i dag lad os holde det rigtigt.)

logaritmisk multiplikation er mægtig sjov

hvor lang tid tager det at vokse 9 gange dit nuværende beløb? Sikker på, vi kunne bare bruge ln (9). Men det er for nemt, lad os være anderledes.

Vi kan overveje 9 gange vækst som tredobling (tager $\ln(3)$ tidsenheder) og derefter tredobling igen (tager en anden $ \ ln (3)$ tidsenheder):

• tid til at vokse 9 gange = $ \ ln (9)$ = tid til tredobbelt og tredobbelt igen = $\ln(3) + \ln(3)$

interessant. Ethvert væksttal, som 20, kan betragtes som 2 gange vækst efterfulgt af 10 gange vækst. Eller 4 gange vækst efterfulgt af 5 gange vækst. Eller 3 gange vækst efterfulgt af 6.666 gange vækst. Kan du se mønsteret?

• $\ln(a*b) = \ln(a) + \ln(B)$

loggen af A gange B = log(a) + log(B). Dette forhold giver mening, når du tænker på tid til at vokse.

hvis vi vil vokse 30 gange, kan vi vente $ \ ln(30) $på en gang, eller bare vente$ \ln(3)$, til tredobbelt, så vent$ \ln (10)$, for at vokse 10 gange igen. Nettoeffekten er den samme, så nettotiden skal også være den samme (og den er).

hvad med division? $ \ ln (5/3)$ betyder: Hvor lang tid tager det at vokse 5 gange og derefter tage 1/3 af det?

Nå, vokser 5 gange er $ \ ln (5)$. Voksende 1/3 er $- \ ln (3)$ enheder af tid. Så

• $\ln(5/3) = \ln(5) – \ln(3)$

som siger: vokse 5 gange og “gå tilbage i tiden”, indtil du har en tredjedel af det beløb, så du er tilbage med 5/3 vækst. Generelt har vi

• $\ln (a / b) = \ln (a) – \ln (b)$

Jeg håber, at den mærkelige matematik af logaritmer begynder at give mening: multiplikation af vækst bliver tilsætning af tid, opdeling af vækst bliver subtraktion af tid. Husk ikke reglerne, forstå dem.

brug af naturlige logfiler med enhver Sats

“sikker på,” siger Du, ” denne log ting virker for 100% vækst, men hvad med de 5%, jeg normalt får?”

det er ikke noget problem. “Tiden” vi kommer tilbage fra $ \ ln ()$ er faktisk en kombination af sats og tid, “H” fra vores $e^$ ligning. Vi antager bare 100% for at gøre det enkelt, men vi kan bruge andre tal.

Antag, at vi vil have 30 gange vækst: tilslut $\ln(30)$ og få 3.4. Det betyder:

• $e^ = \tekst{vækst}$
• $e^{3.4} = 30$

og intuitivt betyder denne ligning “100% afkast i 3,4 år er 30 gange vækst”. Vi kan betragte ligningen som:

Vi kan ændre “rate” og “time”, så længe rate * time = 3.4. Antag for eksempel, at vi vil have 30 gange vækst-hvor længe venter vi på at antage 5% afkast?

• $\ln(30) = 3.4$
• $\tekst{rate} * \tekst{time} = 3.4$
• $.05 * \ tekst{time} = 3.4$
• $\tekst{time} = 3.4 / .05 = 68 \tekst{år}$

intuitivt tror jeg “$\ln(30) = 3,4$, så ved 100% vækst vil det tage 3,4 år. Hvis jeg fordobler væksten, halverer jeg den nødvendige tid.”

• 100% i 3,4 år = 1,0 * 3,4 = 3,4
• 200% i 1,7 år = 2,0 * 1,7 = 3,4
• 50% i 6,8 år = 0,5 * 6,8 = 3,4
• 5% i 68 år = .05 * 68 = 3, 4

Cool, eh? Den naturlige log kan bruges med enhver rente eller tid, så længe deres produkt er det samme. Du kan vrikke variablerne alt hvad du vil.

fantastisk eksempel: reglen om 72

reglen om 72 er en mental matematikgenvej til at estimere den tid, der er nødvendig for at fordoble dine penge. Vi kommer til at udlede det (yay!) og endnu bedre, vi vil forstå det intuitivt.

hvor lang tid tager det at fordoble dine penge med 100% rente, sammensat hvert år?

Uh oh. Vi har brugt naturlig log til kontinuerlige satser, men nu beder du om årlig interesse? Vil det ikke ødelægge vores formel? Ja, det vil, men til rimelige renter som 5%, 6% eller endda 15%, er der ikke meget forskel mellem årlig sammensat og fuldt kontinuerlig rente. Så den grove formel virker, uh, groft og vi vil lade som om vi får fuld kontinuerlig interesse.

nu er spørgsmålet nemt: hvor lang tid at fordoble med 100% interesse? ln(2) = .693. Det tager .693 tidsenheder (år, i dette tilfælde) for at fordoble dine penge med kontinuerlig sammensætning med en sats på 100%.

Ok, hvad hvis vores interesse ikke er 100% Hvad hvis det er 5% eller 10%?

enkel. Så længe Sats * tid = .693, vi fordobler vores penge:

• rate * time = .693
• tid = .693 / rate

så hvis vi kun havde 10% vækst, ville det tage .693 / .10 eller 6,93 år at fordoble.

for at forenkle tingene, lad os gange med 100, så vi kan tale om 10 snarere end .10:

• tid til at fordoble = 69.3 / sats, hvor Sats antages at være i procent.

nu er tiden til at fordoble ved 5% vækst 69,3/5 eller 13,86 år. 69,3 er dog ikke det mest delelige tal. Lad os vælge en nær nabo, 72, som kan divideres med 2, 3, 4, 6, 8 og mange flere tal.

• tid til dobbelt = 72/rate

hvilket er reglen om 72! Let luftig.

Hvis du vil finde tiden til tredobbelt, vil du bruge ln(3) ~ 109,8 og få

• tid til tredobbelt = 110 / rate

hvilket er en anden nyttig tommelfingerregel. Reglen om 72 er nyttig til renter, befolkningsvækst, bakteriekulturer og alt, hvad der vokser eksponentielt.

hvor skal man herfra?

Jeg håber, at den naturlige log giver mere mening-den fortæller dig den tid, der er nødvendig for enhver mængde eksponentiel vækst. Jeg betragter det som” naturligt”, fordi e er den universelle vækstrate, så ln kunne betragtes som den” universelle ” måde at finde ud af, hvor lang tid det tager at vokse.

Når du ser $\ln(h)$, skal du bare tænke “mængden af tid til at vokse til H”. I den næste artikel bringer vi e og ln sammen, og den søde aroma af matematik vil fylde luften.

Appendiks: den naturlige Log af E

Hurtig spørgsmål: Hvad er $ \ ln (e)$?

• matematikrobotten siger: fordi de er defineret til at være inverse funktioner, klart $\ln (e) = 1$
• det intuitive menneske: ln (e) er den tid, det tager at få “e” vækstenheder (ca.2.718). Men e er mængden af vækst efter 1 tidsenhed, så $\ln(e) = 1$.

tænk intuitivt.

andre indlæg i denne serie

1. en intuitiv Guide til eksponentielle funktioner & e
2. afmystificering af den naturlige logaritme (ln)
3. en visuel Guide til enkle, sammensatte og kontinuerlige renter
4. almindelige definitioner af e (farvet)
5. forståelse af eksponenter (hvorfor gør 0^0 = 1?)
6. brug af logaritmer i den virkelige verden
7. Sådan tænker du med eksponenter og logaritmer
8. forståelse diskret vs. kontinuerlig vækst
9. hvad betyder en eksponent virkelig?
10. spørgsmål: Hvorfor er e speciel? (2.718…, ikke 2, 3.7 eller et andet nummer?)