i andre afsnit blev det nævnt, at mange af egenskaberne af faste stoffer, væsker og gasser kunne redegøres for, hvis vi antog, at stoffer er lavet af atomer eller molekyler, der konstant er i bevægelse. Boyles lov og de andre gaslove har nu givet os meget mere kvantitativ information om gasser, og det er værd at spørge, om vi med den tidligere model kan foretage kvantitative forudsigelser i overensstemmelse med disse love. Når vi besvarer dette spørgsmål, får vi også vigtig indsigt i temperaturens og varmeenergiens Art.

den mikroskopiske teori om gasadfærd baseret på molekylær bevægelse kaldes den kinetiske teori om gasser. Dens grundlæggende postulater er anført i tabel 1:

tabel \(\Sideindeks{1}\) postulater af den kinetiske teori om gasser.

1 molekylerne i en gas er små og meget langt fra hinanden. Det meste af det volumen, som en gas optager, er tomt rum.

2 gasmolekyler er i konstant tilfældig bevægelse. Lige så mange molekyler bevæger sig i en retning som i enhver anden.

3 molekyler kan kollidere med hinanden og med beholderens vægge. Kollisioner med væggene tegner sig for gasens tryk.

4 Når kollisioner opstår, mister molekylerne ingen kinetisk energi; det vil sige, at kollisionerne siges at være perfekt elastiske. Den samlede kinetiske energi af alle molekylerne forbliver konstant, medmindre der er nogen udefrakommende interferens med

5 molekylerne udøver ingen attraktive eller frastødende kræfter på hinanden undtagen under kollisionsprocessen. Mellem kollisioner bevæger de sig i lige linjer.

fra dem er det muligt at udlede følgende udtryk for trykket af en gas med hensyn til egenskaberne af dets molekyler:

\ hvor P, V = tryk og volumen af gassen

N = antal molekyler

M = Masse af hvert molekyle

(u2)ave = gennemsnit (eller gennemsnit) af kvadraterne af alle individuelle molekylhastigheder. Denne gennemsnitlige kvadrathastighed skal bruges, fordi trykket er proportionalt med kvadratet af molekylær hastighed, og molekylære kollisioner får forskellige molekyler til at have helt forskellige hastigheder.

i stedet for at beskæftige os med proceduren for at udlede EKV. \(\ref{1}\), Lad os inspicere ligningen og se, at dens generelle funktioner er meget, som vi ville forvente. På nogle måder er evnen til at gøre dette med en formel mere nyttig end evnen til at udlede den. Figur \(\Sideindeks{1}\)

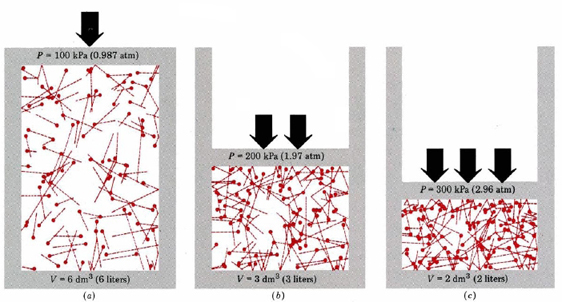først og fremmest fortæller ligningen os, at trykket af en gas er proportional med antallet af molekyler divideret med volumenet. Dette vises grafisk i figur \(\Sideindeks{1}\), hvor en computer har tegnet det samme antal gasmolekyler, der optager hver af tre forskellige volumener. “Halen” på hvert molekyle viser den nøjagtige sti efterfulgt af molekylet i det foregående mikrosekund—jo længere halen var, jo hurtigere gik molekylet. Gennemsnittet af kvadraterne på halelængderne er proportional med (u2)ave og er det samme i alle tre diagrammer. Det antages også, at alle molekylerne har lige masser.

som du kan se, reducerer gasens volumen antallet af kollisioner pr. Hver kollision udøver kraft på væggen; kraft pr.arealenhed er tryk, og derfor er antallet af kollisioner pr. arealenhed proportional med trykket. Halvering af volumen fordobler trykket, en forudsigelse, der stemmer overens med de eksperimentelle fakta, der er opsummeret i Boyles lov. Ligning \(\ref{1}\) siger også, at trykket er proportional med massen af hvert gasmolekyle. Igen er det, hvad vi ville forvente. Tunge molekyler giver et større”skub” (det tekniske udtryk for dette er impuls) mod væggen end lys med samme hastighed.

endelig fortæller ligningen os, at trykket er proportional med gennemsnittet af kvadraterne af molekylhastighederne. Denne afhængighed af kvadratet af hastighed er rimelig, hvis vi indser, at fordobling af hastigheden af et molekyle har to effekter.

for det første kan molekylet bevæge sig længere i en given tidsperiode og fordoble antallet af kollisioner med væggene. Det vil fordoble presset. For det andet fordobler fordoblingen af et molekyles hastighed push eller impuls for hver kollision. Dette fordobler trykket igen. Derfor fordobler et molekyles hastighed trykket, og for et stort antal molekyler er P proportional med den gennemsnitlige kvadrathastighed.