Boyles lov
Robert Boyle (1627 – 1691), en engelsk kemiker, anses bredt for at være en af grundlæggerne af den moderne eksperimentelle videnskab om kemi. Han opdagede, at fordobling af trykket fra en lukket gasprøve, mens temperaturen holdes konstant, fik gasens volumen til at blive reduceret med halvdelen. Boyles lov siger, at volumenet af en given gasmasse varierer omvendt med trykket, når temperaturen holdes konstant. Et omvendt forhold beskrives på denne måde. Når en variabel stiger i værdi, falder den anden variabel.
fysisk, Hvad sker der? Gasmolekylerne bevæger sig og er en vis afstand fra hinanden. En stigning i tryk skubber molekylerne tættere sammen, hvilket reducerer volumenet. Hvis trykket falder, er gasserne fri til at bevæge sig rundt i et større volumen.

matematisk kan Boyles lov udtrykkes ved ligningen:
\
\(k\) er en konstant for en given gasprøve og afhænger kun af gasens masse og temperaturen. Tabellen nedenfor viser Tryk-og volumendata for en bestemt mængde gas ved en konstant temperatur. Den tredje kolonne repræsenterer værdien af konstanten \(\venstre (k \højre)\) for disse data og er altid lig med trykket multipliceret med lydstyrken. Når en af variablerne ændres, ændres den anden på en sådan måde, at produktet af \(P \times V\) altid forbliver det samme. I dette særlige tilfælde er denne konstant \(500 \: \tekst{atm} \ cdot \ tekst{mL}\).
| Pressure \(\left( \text{atm} \right)\) | Volume \(\left( \text{mL} \right)\) | \(P \times V = k\) \(\left( \text{atm} \cdot \text{mL} \right)\) |
|---|---|---|
| 0.5 | 1000 | 500 |
| 0.625 | 800 | 500 |
| 1.0 | 500 | 500 |
| 2.0 | 250 | 500 |
| 5.0 | 100 | 500 |
| 8.0 | 62.5 | 500 |
| 10.0 | 50 | 500 |
en graf over dataene i tabellen illustrerer yderligere det omvendte forhold karakter af Boyles lov (se figur nedenfor). Volumen er tegnet på \(h\)-aksen, med det tilsvarende tryk på\(y\)-aksen.
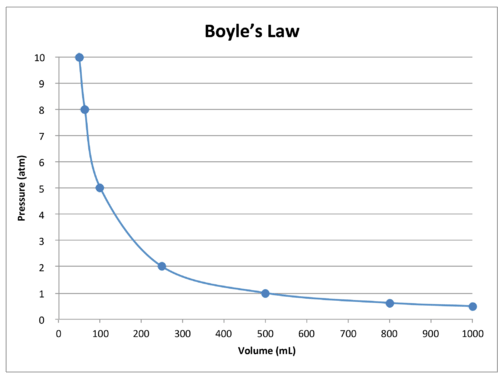
Boyles lov kan bruges til at sammenligne skiftende forhold for en gas. Vi bruger \(P_1\) og \(V_1\) til at stå for det indledende tryk og indledende volumen af en gas. Når en ændring er foretaget, står \(P_2\) og \(V_2\) for det endelige tryk og volumen. Det matematiske forhold mellem Boyles lov bliver:
\
denne ligning kan bruges til at beregne en af de fire mængder, hvis de andre tre er kendt.
eksempel \(\Sideindeks{1}\)
en prøve af iltgas har et volumen på \(425 \: \tekst{mL}\) når trykket er lig med \(387 \: \tekst{kPa}\). Gassen får lov til at ekspandere til en \(1,75 \: \tekst{L}\) beholder. Beregn Det Nye tryk på gassen.
løsning
Trin 1: Angiv de kendte mængder, og planlæg problemet.
kendt
- \(P_1 = 387 \: \tekst{kPa}\)
- \(V_1 = 425 \: \tekst{mL}\)
- \(V_2 = 1.75 \: \tekst{L} = 1750 \: \tekst{mL}\)
ukendt
- \(p_2 = ? \ : \ tekst{kPa}\)
brug Boyles lov til at løse for det ukendte Tryk \(\venstre( P_2 \højre)\). Det er vigtigt, at de to bind (\(V_1\) og \(V_2\)) udtrykkes i de samme enheder, så \(V_2\) er konverteret til \(\tekst{mL}\).
Trin 2: Løs.
Omarranger først ligningen algebraisk for at løse for \(P_2\).
\
nu erstatte de kendte mængder i ligningen og løse.
\
Trin 3: Tænk på dit resultat.
volumenet er steget til lidt over 4 gange dets oprindelige værdi, og derfor reduceres trykket med ca.en fjerdedel. Trykket er i \(\tekst{kPa}\), og værdien har tre signifikante tal. Bemærk, at alle tryk-eller volumenenheder kan bruges, så længe de er konsistente i hele problemet.