atomorbitaler
en orbital er den kvantemekaniske forfining af Bohrs bane. I modsætning til hans koncept om en simpel cirkulær bane med en fast radius er orbitaler matematisk afledte rumområder med forskellige sandsynligheder for at have en elektron.
en måde at repræsentere elektron sandsynlighedsfordelinger blev illustreret i figur 6.5.2 for 1s orbital af hydrogen. Fordi Lus2 giver sandsynligheden for at finde en elektron i et givet rumfang (såsom et kubisk picometer), er et plot af Lus2 versus afstand fra kernen (r) et plot af sandsynlighedstætheden. 1s-orbitalen er sfærisk symmetrisk, så sandsynligheden for at finde en 1s-elektron på et givet tidspunkt afhænger kun af dens afstand fra kernen. Sandsynlighedstætheden er størst ved r = 0 (ved kernen) og falder støt med stigende afstand. Ved meget store værdier af r er elektronsandsynlighedstætheden meget lille, men ikke nul.i modsætning hertil kan vi beregne den radiale Sandsynlighed (sandsynligheden for at finde en 1s − elektron i en afstand r fra kernen) ved at tilføje sandsynlighederne for, at en elektron er på alle punkter på en række sfæriske skaller med radius r1, r2, r3,…, RH-1, RH. I virkeligheden deler vi atomet i meget tynde koncentriske skaller, ligesom lagene af en løg (del (A) i figur \(\Sideindeks{1}\)) og beregner sandsynligheden for at finde en elektron på hver sfærisk skal. Husk, at elektronens sandsynlighedstæthed er størst ved r = 0 (del (b) i figur \(\Sideindeks{1}\)), så tætheden af prikker er størst for de mindste sfæriske skaller delvist (a) i figur \(\Sideindeks{1}\). I modsætning hertil er overfladearealet af hver sfærisk skal lig med 4nr2, hvilket øges meget hurtigt med stigende r (del (c) i figur \(\Sideindeks{1}\)). Fordi overfladearealet af de sfæriske skaller stiger hurtigere med stigende r end elektronens sandsynlighedstæthed falder, har plottet af radial Sandsynlighed et maksimum i en bestemt afstand (del (d) i figur \(\Sideindeks{1}\)). Vigtigst, når r er meget lille, er overfladearealet af en sfærisk skal så lille, at den samlede sandsynlighed for at finde en elektron tæt på kernen er meget lav; ved kernen forsvinder elektronsandsynligheden (del (d) i figur \(\Sideindeks{1}\)).

for hydrogenatomet forekommer toppen i det radiale sandsynlighedsplot ved r = 0,529 liter (52,9 pm), hvilket er nøjagtigt den radius, der beregnes af Bohr for N = 1 bane. Således er den mest sandsynlige radius opnået fra kvantemekanik identisk med radius beregnet af klassisk mekanik. I Bohrs model blev elektronen imidlertid antaget at være på denne afstand 100% af tiden, mens det i den kvantemekaniske Schr-Kristinger-model kun er på denne afstand noget af tiden. Forskellen mellem de to modeller kan henføres til elektronens bølgelignende opførsel og Heisenberg usikkerhedsprincippet.
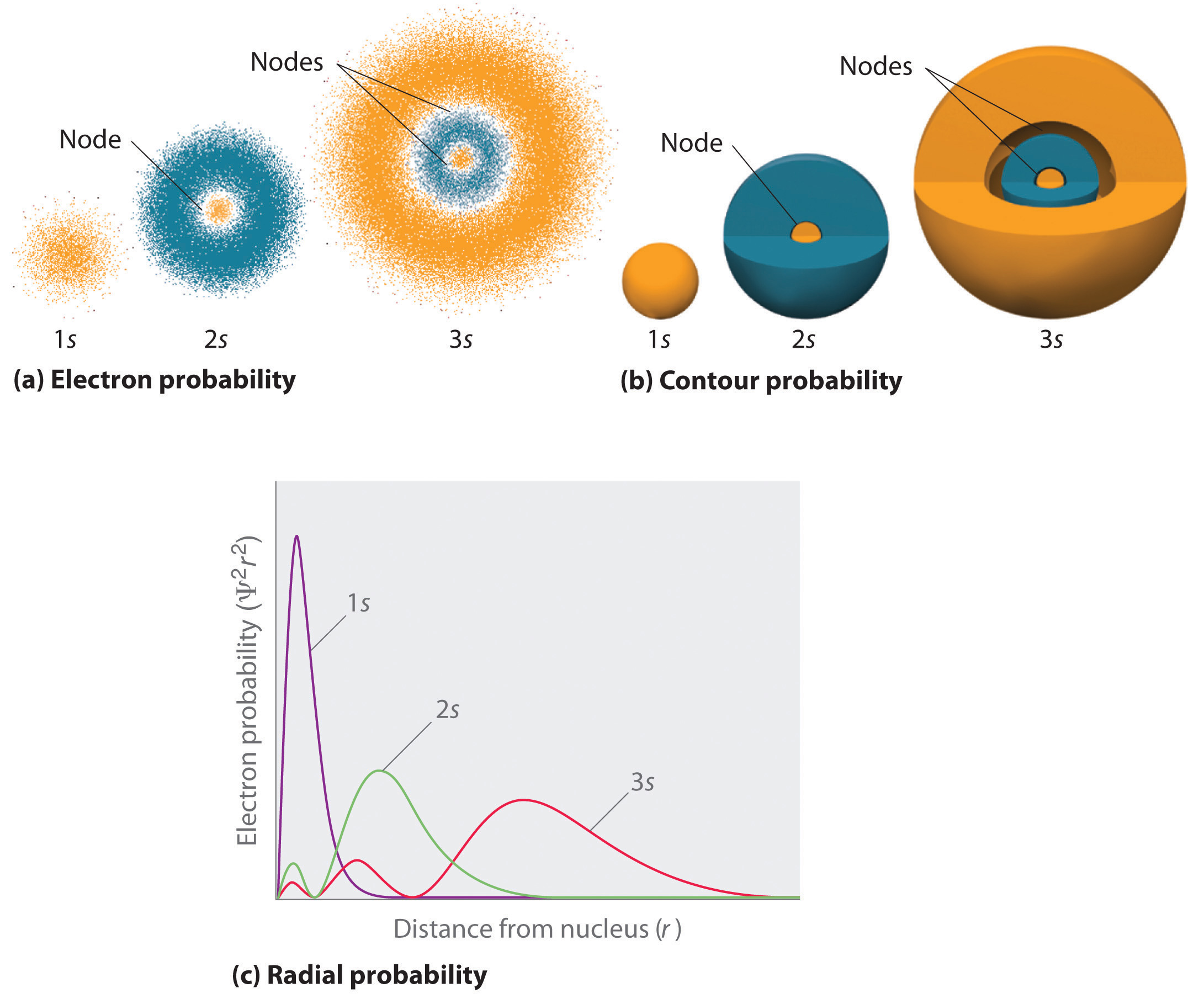
figur \(\Sideindeks{2}\) sammenligner elektronens sandsynlighedstætheder for hydrogen 1s, 2s og 3s orbitaler. Bemærk, at alle tre er sfærisk symmetriske. For 2s-og 3S-orbitalerne (og også for alle andre s-orbitaler) falder elektronsandsynlighedstætheden ikke glat med stigende r. i stedet observeres en række minima og maksima i de radiale sandsynlighedsplotter (del (c) i figur \(\Sideindeks{2}\)). Minima svarer til sfæriske noder (regioner med nul elektronsandsynlighed), som veksler med sfæriske regioner med ikke-nul elektronsandsynlighed.