Purplemath
v matematice je“ identita “ rovnice, která je vždy pravdivá. Ty mohou být „triviálně“ pravdivé, jako „x = x“ nebo užitečně pravdivé, jako je Pythagorova věta „a2 + b2 = c2“ pro pravoúhlé trojúhelníky. Existuje spousta trigonometrických identit, ale následující jsou ty, které s největší pravděpodobností uvidíte a použijete.
Basic & Pythagorean, Angle-Sum & -Difference, Double-Angle, Half-Angle, Sum, Product
Content Continues Below
MathHelp.com
Need a custom math course?
K12 | College | Test Prep

Základní a Pythagorean Identity
Affiliate
Všimněte si, jak „co-(něco)“trig poměr je vždy reciproční některých „ne-spolupráci“ poměr. Můžete použít tuto skutečnost, která vám pomůže udržet rovně, že kosekant jde s sinus a sekant jde s kosinus.
následující (zejména první ze tří níže) se nazývají „Pythagorejské“ identity.
sin2(t) + cos2(t) = 1
tan2(t) + 1 = s2(t)
1 + cot2(t) = csc2(t)
Reklama
Všimněte si, že tři identity především zahrnovat kvadratura a číslo 1. Můžete vidět, Pythagorova-Thereom vztah jasně, pokud se domníváte, jednotkové kružnice, kde je úhel t, „opačné“ straně je sin(t) = y, „sousední“ strana je cos(t) = x, a přepony je 1.
Máme další identity týkající se funkční stav trig poměry:
sin(–t) = –sin(t),
cos(–t) = cos(t),
tan(–t) = –tan(t),
Všimněte si zejména, že sinus a tangens je lichá funkce, být symetrické o původu, zatímco kosinus je sudá funkce, je symetrický podle osy y. Skutečnost, že můžete vzít znaménko „mínus“ argumentu venku (pro sinus a tečnu) nebo jej úplně odstranit (pro kosinus), může být užitečná při práci s komplikovanými výrazy.
Úhel Součet a Rozdíl Identity
sin(α + β) = sin(α) cos(β) + cos(α) sin(β)
sin(α – β) = sin(α) cos(β) – cos(α) sin(β)
cos(α + β) = cos(α) cos(β) – sin(α) sin(β)
cos(α – β) = cos(α) cos(β) + sin(α) sin(β)
mimochodem, ve výše uvedených identit, úhly jsou označeny řeckými písmeny. Písmeno typu a,“ α“, se nazývá“ alfa“, což se vyslovuje“AL-fuh“. Písmeno typu B, „β“, se nazývá „beta“, což se vyslovuje „BAY-tuh“.
Obsah Pokračuje Níže
Double-Úhel Identity
sin(2x) = 2 sin(x) cos(x)
cos(2x) = cos2(x) – sin2(x) = 1 – 2 sin2(x) = 2 cos2(x) – 1
Half-Úhel Identity
výše uvedené identity může být re-uvedl kvadratura každé straně a zdvojnásobení všech úhel opatření. Výsledky jsou následující:
Affiliate

Sum Identities
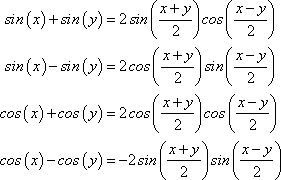
Product Identities
Affiliate
Budete používat všechny tyto identity, nebo téměř tak, pro prokázání dalších trigonometrii a pro řešení goniometrických rovnic. Nicméně, pokud se chystáte na studium kalkul, věnovat zvláštní pozornost úpravě sinus a kosinus half-úhel identity, protože budete používat je hodně integrální počet.
URL: https://www.purplemath.com/modules/idents.htm