Souřadnicové Roviny
Učení Cíl(y),
· Plot objednané páry na souřadnicové rovině.
* vzhledem k uspořádanému páru určete jeho kvadrant.
Úvod
souřadnicové roviny byla vyvinuta již před staletími a rafinovaný francouzský matematik René Descartes. Na jeho počest se systém někdy nazývá Kartézský souřadnicový systém. Souřadnicovou rovinu lze použít k vykreslení bodů a čar grafu. Tento systém nám umožňuje popsat algebraické vztahy ve vizuálním smyslu a také nám pomáhá vytvářet a interpretovat algebraické pojmy.
seznámení se s rovinou souřadnic
pravděpodobně jste dříve použili rovinu souřadnic. Například, už jste někdy použili překrytí mřížkou k mapování polohy objektu? (Často se tak děje i u silničních map.)

Tato „mapa“ používá horizontální a vertikální mřížky zprostředkovat informace o umístění objektu. Všimněte si, že písmena A-F jsou uvedena nahoře a čísla 1-6 jsou uvedena podél levého okraje. Obecné umístění jakékoli položky na této mapě lze nalézt pomocí písmene a čísla čtverce mřížky. Například, můžete najít položku, která existuje na náměstí „4F“ pohybem prstu po horizontální pro písmeno F, a pak rovnou dolů, takže jste v souladu s 4. Na tomto místě na mapě najdete modrý disk.
rovina souřadnic má podobné prvky jako výše uvedená mřížka. Skládá se z vodorovné osy a svislé osy, číselných čar, které se protínají v pravém úhlu. (Jsou na sebe kolmé.)
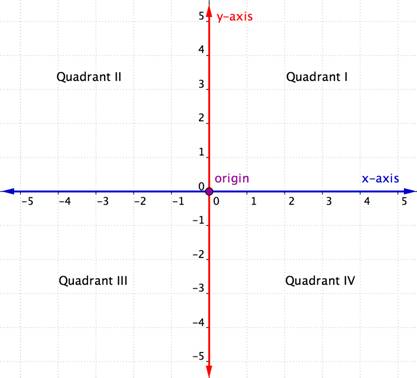
vodorovná osa v rovině souřadnic se nazývá osa x. Svislá osa se nazývá osa y. Bod, ve kterém se obě osy protínají, se nazývá původ. Počátek je 0 na ose x a 0 na ose y.
protínající se osy x a y dělí rovinu souřadnic na čtyři sekce. Tyto čtyři sekce se nazývají kvadranty. Kvadranty jsou pojmenovány římskými číslicemi I, II, III, a IV začínající pravým horním kvadrantem a pohybující se proti směru hodinových ručiček.
místa v rovině souřadnic jsou popisována jako uspořádané páry. Uspořádaná dvojice vám řekne, umístění bodu, o bod je místo podél osy x (první hodnota objednaného pár) a podél osy y (druhá hodnota objednaného pár).
v uspořádaném páru, jako je (x, y), se první hodnota nazývá x-souřadnice a druhá hodnota je Y-souřadnice. Všimněte si, že souřadnice x je uvedena před souřadnicí y. Protože Počátek má souřadnici x 0 a souřadnici y 0, je zapsán jeho uspořádaný pár (0, 0).
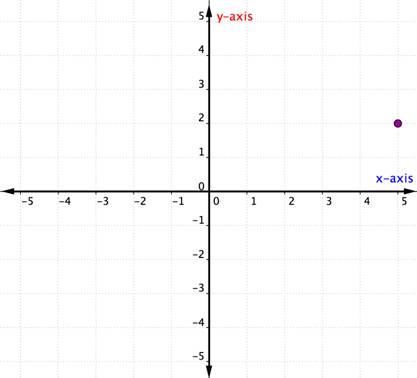
zvažte níže uvedený bod.
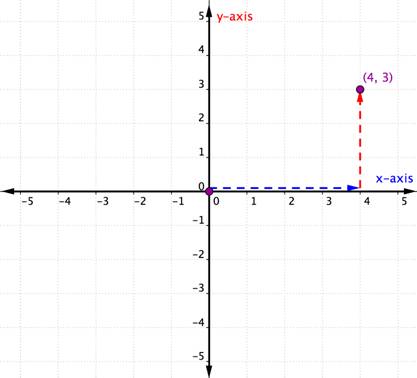
určit umístění tohoto bodu, začít na počátku (0, 0) a pohybovat vpravo na ose x, dokud jste pod bod. Podívejte se na štítek na ose x. 4 znamená, že od počátku jste cestovali čtyřmi jednotkami doprava podél osy x. Toto je souřadnice x, první číslo v objednaném páru.
od 4 na ose x se přesuňte nahoru k bodu A všimněte si čísla, se kterým se zarovná na ose y. 3 znamená, že po opuštění osy x jste cestovali 3 jednotky nahoru ve svislém směru, ve směru osy y. Toto číslo je souřadnice y, druhé číslo v objednaném páru. S X-souřadnicí 4 a Y-souřadnicí 3 Máte uspořádaný pár (4, 3).
podívejme se na jiný příklad.
|
Example |
||
|
Problem |
Describe the point shown as an ordered pair. |
|
|
|
||
|
(5, y) |
Začněte na původ a pohybovat podél osy x. Toto je souřadnice x a je zapsána jako první v uspořádaném páru. |
|
|
(5, 2) |
Pohybovat od 5 až do nařízeno pár, a přečtěte si číslo na ose y. Toto je souřadnice y a je zapsána jako druhá v uspořádaném páru. |
|
|
Odpovědět |
bod zobrazen jako uspořádaná dvojice (5, 2). |
|
Spiknutí Body v Souřadnicové Roviny
Nyní, když víte, jak používat x – a y-osy, můžete plot uspořádané dvojice stejně. Jen si pamatujte, že oba procesy začínají na počátku-na začátku! Následující příklad ukazuje, jak grafovat uspořádaný pár (1, 3).
|
Example |
||
|
Problem |
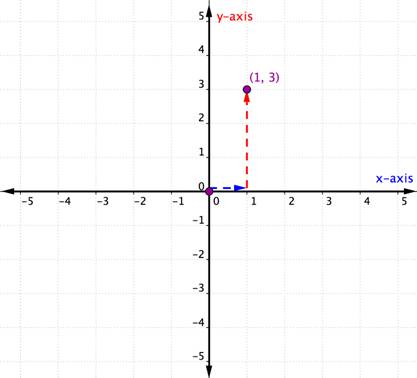
Plot the point (1, 3). |
|
|
|
||
|
The x-coordinate is 1 because it comes first in the ordered pair. Začněte Od počátku a přesuňte vzdálenost 1 jednotky v kladném směru (doprava) Od počátku podél osy x. |
souřadnice y je 3, protože je druhá v uspořádaném páru. Odtud se přesuňte přímo 3 jednotky v pozitivním směru (nahoru). Pokud se podíváte na osu y, měli byste být seřazeni s 3 na této ose. |
|
|
Odpovědět |
Nakreslit bod na tomto místě a označit bod (1, 3). |
|
v předchozím příkladu byly souřadnice x I y kladné. Pokud je jedna (nebo obě) souřadnic uspořádaného páru záporná, budete se muset pohybovat v záporném směru podél jedné nebo obou OS. Zvažte níže uvedený příklad, ve kterém jsou obě souřadnice záporné.
|
Example |
||
|
Problem |
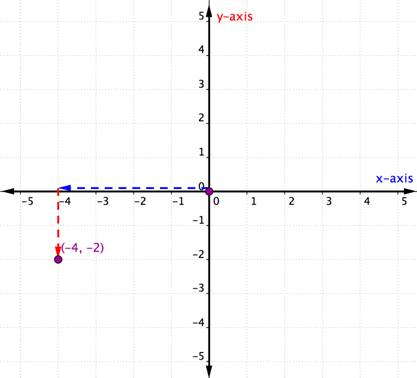
Plot the point (−4, −2). |
|
|
|
||
|
The x-coordinate is −4 because it comes first in the ordered pair. Začněte Od počátku a přesuňte 4 jednotky v záporném směru (vlevo) podél osy x. |
souřadnice y je -2, protože je druhá v uspořádaném páru. Nyní přesuňte 2 jednotky v záporném směru (dolů). Pokud se podíváte na osu y, měli byste být seřazeni s -2 na této ose. |
|
|
Odpovědět |
Nakreslit bod na tomto místě a označit bod (-4, -2). |
|
kroky pro vykreslení bodu jsou shrnuty níže.
kroky pro vynesení uspořádaného páru (x, y) v rovině souřadnic
O Určete souřadnici x. Počínaje počátkem se pohybujte vodorovně, směr osy x, vzdálenost daná souřadnicí x. Pokud je souřadnice x kladná, přesuňte se doprava; pokud je souřadnice x záporná, přesuňte se doleva.
O Určete souřadnici y. Počínaje souřadnicí x se pohybujte svisle, směrem osy y, vzdáleností danou souřadnicí y. Pokud je souřadnice y kladná, posuňte se nahoru; pokud je souřadnice y záporná, posuňte se dolů.
o nakreslete bod na koncovém místě. Označte bod objednaným párem.
který bod představuje uspořádaný pár (-2, -3)?
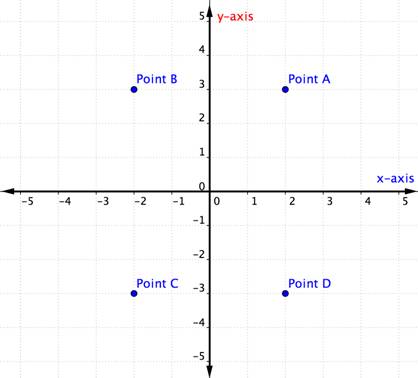
Čtyři Kvadranty
Objednané páry rámci dané kvadrantu sdílejí určité charakteristiky. Podívejte se na každý kvadrant v grafu níže. Co si všimnete o znameních souřadnic x a y bodů v každém kvadrantu?
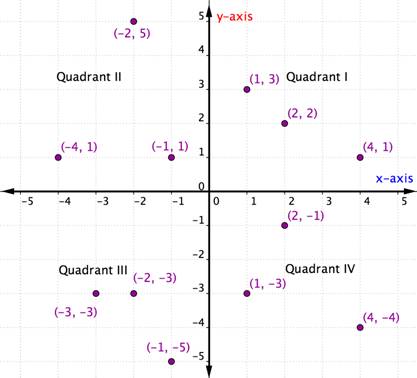
v Rámci každého kvadrantu, znamení x-souřadnice, y-souřadnice každého nařídil dvojice jsou stejné. Sledují také vzor, který je uveden v následující tabulce.
jakmile víte o kvadrantech v souřadnicové rovině, můžete určit kvadrant uspořádaného páru, aniž byste jej vykreslili, a to při pohledu na výše uvedený graf. Zde je další způsob, jak o tom přemýšlet.
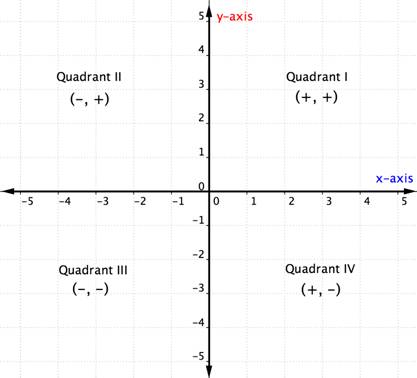
níže uvedený příklad popisuje, jak určit kvadrant umístění bodu jen tím, přemýšlet o příznaky jeho souřadnice. Přemýšlení o umístění kvadrantu před vykreslením bodu vám může pomoci zabránit chybě. Je také užitečné znalosti pro kontrolu, že jste vynesli bod správně.
Co se stane, když uspořádaný pár má souřadnici X nebo y nula? Níže uvedený příklad ukazuje graf uspořádaného páru (0, 4).
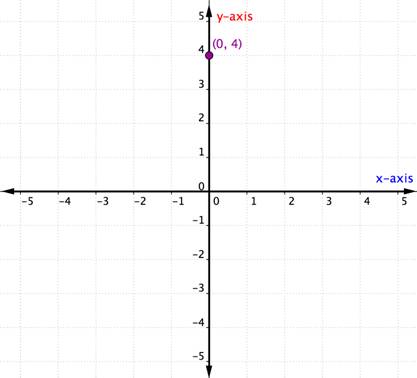
bod umístěný na jedné z OS se nepovažuje za kvadrant. Je to prostě na jedné z OS. Kdykoli je souřadnice x 0, bod je umístěn na ose y. Podobně každý bod, který má souřadnici y 0, bude umístěn na ose x.
který z níže uvedených popisů nejlépe popisuje umístění bodu (8, 0)?
A) Kvadrantu.
B) je na ose x
C) je na ose y
D) Souřadnicové roviny
Shrnutí
souřadnicové roviny je systém pro vytváření grafů a popisu bodů a čar. Souřadnicová rovina se skládá z vodorovné (X -) osy a svislé (y-) osy. Průsečík těchto čar vytváří Počátek, kterým je bod (0, 0). Rovina souřadnic je rozdělena do čtyř kvadrantů. Spolu, tyto vlastnosti souřadného systému umožňují grafické znázornění a komunikace o body, čáry a další algebraické pojmy.