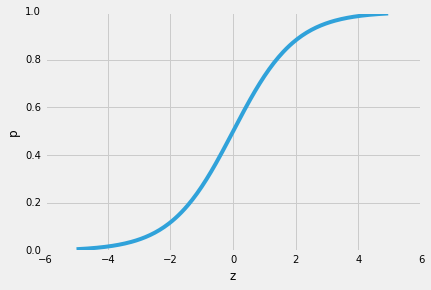
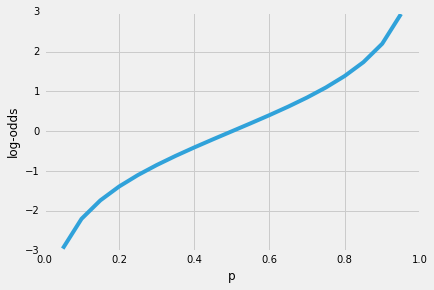
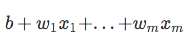jednou z pěkných vlastností logistické regrese je, že sigmoid funkce výstupy podmíněnou pravděpodobnost predikce, třída pravděpodobnosti. Jak to funguje?Pojďme začít s tzv. „odds ratio“ p / (1 – p), který popisuje poměr mezi pravděpodobností, že určitý, pozitivní, události a pravděpodobnosti, že nenastane – kde pozitivní odkazuje na „případě, že chceme předpovědět“, tj. p(y=1 | x).
(Všimněte si, že logistická regrese zvláštní druh sigmoidní funkce, logistický sigmoid; existují i jiné sigmoidní funkce, například hyperbolická tečna).
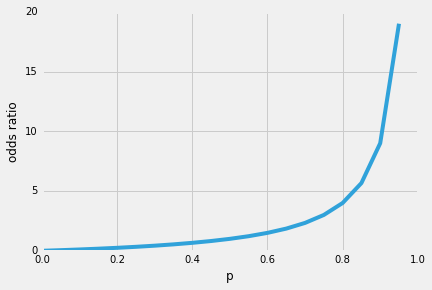
takže čím je pravděpodobnější, že dojde k pozitivní události, tím větší je poměr šancí.Nyní, pokud vezmeme přirozený logaritmus tohoto odds ratio, log-odds nebo logit funkce, dostaneme následující
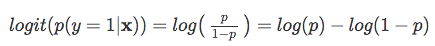
Next, pojďme použít tento log transformace do modelu vztahu mezi vysvětlující proměnné a cílovou proměnnou:
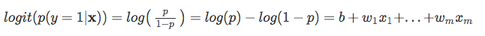
| Nyní, aby to paměti, že nejsme snaží předvídat pravé části rovnice výše, od *p(y=1 | x)* je to, co nás opravdu zajímá. So, let’s take the inverse of this logit function … et viola, we get the logistic sigmoid: |
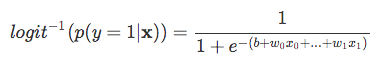
| which returns the class probabilities *p(y=1 | x)* from the inputs |