tato část zahrnuje:

• Úvod do Funkce po Částech
• Hodnocení po Částech Funkce
• po Částech Grafů Funkcí
• Jak zjistit, zda Funkce je po Částech Spojité nebo nespojité
• Získání Rovnic z po Částech Funkce, Grafy
• Absolutní Hodnota jako po Částech Funkce
• Transformace po Částech Funkce
• po Částech Funkce Slovních úloh
• Více Praxe

po Částech funkce (nebo kus-wise funkce) jsou právě to, co oni jsou pojmenovány: kusy různých funkcí (dílčích funkcí) vše na jednom grafu. Nejjednodušší způsob, jak o nich přemýšlet je, pokud si nakreslil více než jednu funkci na grafu, a vy prostě vymazány části funkce, kde by neměla být (spolu \(x\)’s); jsou definovány různě pro různé intervaly \(x\). \(y\) je definováno odlišně pro různé hodnoty \(x\); pomocí \(x\) vyhledáme, v jakém intervalu je, abychom zjistili, co má být \(y\).

Všimněte si, že zde je příklad inverzní funkce po částech v sekci Inverses of Functions.

Here’s an example and graph:

Piecewise Function

Graph

\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ if }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ if }x>-2\end{align} \right.\) (Existují i jiné způsoby zobrazení, jako je použití „pro“ místo „jestli“, a pomocí čárky nebo středníky místo „jestli“.) Domény: \(\mathbb{R},\,\,\,\text{nebo}\,\,\left( {-\infty ,\infty } \right)\) Rozsah: \(\mathbb{R},\,\,\,\text{nebo}\,\,\left( {-\infty ,\infty } \right)\)

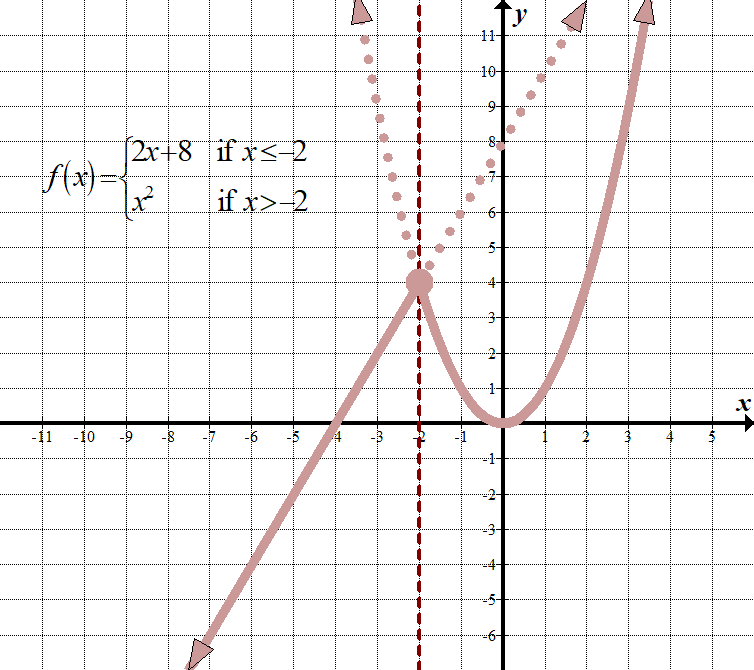Co to znamená pro každé \(x\) je menší než nebo rovna -2, musíme graf řádku \(2x+8\), jako kdyby to byly jen funkce na grafu. Pro každou hodnotu \(x\) větší než -2 musíme graf \({{x}^{2}}\), jako by to byla jediná funkce v grafu. Pak se musíme „zbavit“ částí, které nepotřebujeme. Nezapomeňte, že stále používáme původ jako referenční bod pro oba grafy!

podívejte se, jak svislá čára \(x=-2\) funguje jako“ hraniční “ čára mezi dvěma grafy?

Všimněte si, že bod \((-2,4)\) má uzavřený kruh. Technicky, to by mělo patřit pouze do \(2x+8\) funkce, protože tuto funkci má méně než nebo rovno podepsat, ale od bodu je také na \({{x}^{2}}\) graf, můžeme prostě použít uzavřený kruh, jako kdyby to objeví na obě funkce. Vidíš, není to tak špatné, že?

vyhodnocování funkcí po částech

někdy dostanete funkce po částech a požádáte je o jejich vyhodnocení; jinými slovy, najděte hodnoty \(y\), když dostanete hodnotu \(x\). Udělejme to pro \(x=-6\) a \(x=4\) (bez použití grafu). Zde je funkce znovu:

\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ pokud }x\le -2\\{{x,}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ pokud }x>-2\end{align} \right.\)

nejprve se chceme podívat na podmínky vpravo, abychom zjistili, kde je naše \(x\). Když \(x=-6\), víme, že je menší než -2, takže připojujeme pouze naše \(x\) na \(2x+8\). \(f (x)\) nebo \(y\) je \((2)(-6)+8=-4\). Nestaráme se ani o \(\boldsymbol{{x}^{2}}\)! Je to tak snadné. Můžete také vidět, že jsme to udělali správně pomocí grafu výše.

Nyní zkuste \(x=4\). Nejprve se podíváme doprava a uvidíme, že naše \(x\) je větší než -2, takže jej zapojíme do \({{x}^{2}}\). (Tentokrát můžeme ignorovat \(2x+8\).) \(f (x)\) nebo \(y\) je \({{4}^{2}}=16\).

grafy po částech funkce

pravděpodobně budete požádáni o graf po částech funkce. Grafy někdy obsahují funkce, které nejsou spojité nebo diskontinuální, což znamená, že při kreslení musíte vyzvednout tužku uprostřed grafu (jako skok!). Kontinuální funkce znamená, že nikdy nebudete muset vyzvednout tužku, pokud byste je měli kreslit zleva doprava.

a nezapomeňte, že grafy jsou pravdivé funkce, pouze pokud projdou testem svislé čáry.

nakreslíme tyto funkce po částech a určíme, zda jsou spojité nebo nekontinuální. Všimněte si, jak nakreslíme každou funkci, jako by byla jediná, a poté „vymažeme“ části, které nejsou potřeba. Získáme také oblast a rozsah, jako jsme to udělali zde v sekci algebraických funkcí.

Piecewise Function	Graph
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\left( {0,\infty } \right)\)
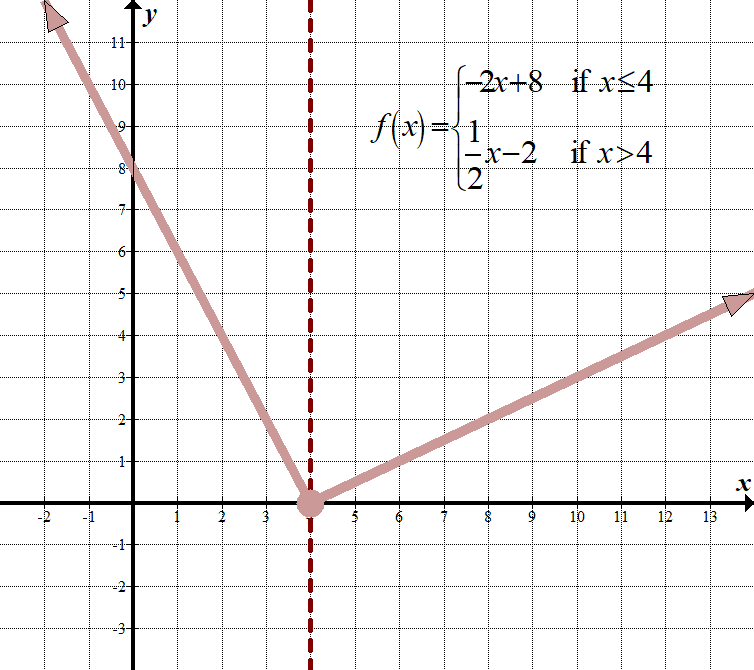\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1}\le x<4\\x-5\,\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\) Non-Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\)

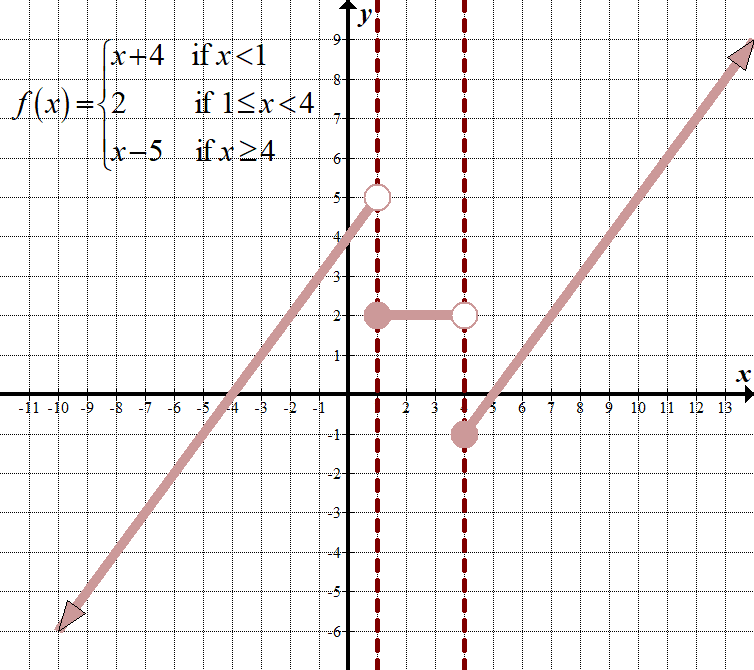We can actually put piecewise functions in the graphing calculator:

Piecewise Function Screens

Steps and Notes

Enter the piecewise function on three lines: Zde je graf:

dát po částech funkce \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{pokud }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{1 }\le x<4\\-5+x\,\,\,\,\,\text{pokud }x\ge 4\end{array} \right.\ ) v kalkulačce můžete zadat funkci na třech řádcích vydělením funkce v každém intervalu „testovací nerovností“ tohoto intervalu (a sledujte závorky!). důvod, proč jsme Se rozdělit do intervalů, nebo nerovnosti je proto, kalkulačka vrátí 1, pokud nerovnost (například \(x<1\)) je pravda; například \((x+4)\), bude prostě skončit \((x+4)/(1)\) až \(x<1\). Když \(x\ge 1\), dělíme 0, takže nic nebude nakresleno. Zde je to, co můžeme dát do kalkulačky: \(\displaystyle \begin{array}{l}{{Y}_{1}}=\left( {x+4} \right)/\left( {x<1} \right)\\{{Y}_{2}}=\left( 2 \right)/\left( {x\ge 1\text{ a }x<4} \right)\\{{Y}_{3}}=\left( {-5+x} \right)/\left( {x\ge 4} \right)\end{array}\) (Všimněte si, že můžete také zadat na jeden řádek vynásobením podmínek namísto rozdělení, a pomocí znaménka plus mezi každou ze tří funkcí/intervaly: \(\displaystyle {{Y}_{1}}=\left( {x+4} \right)\left( {x<1} \right)+\left( 2 \right)\left( {x\ge 1\text{ a }x<4} \right)+\left( {-5+x} \right)\left( {x\ge 4} \right)\).) zde jsou stisknutí kláves pro použití tří řádků. Všimněte si, že používáte 2nd MATH (TEST) se dostat na obrazovku, která má \(\le \), \(\ge\), a tak dále. Například 2. matematika 6 vás dostane \(\le \). Použijte 2. MATH (TEST), právo na logiku, pak 1, Pro „a“ v \({{Y}_{2}}\).

Jak zjistit, zda Funkce je po Částech Spojité nebo nespojité

zjistit, jestli po částech grafu je souvislý nebo nesouvislý, můžete se podívat na hraniční body, a uvidíme, jestli \(y\) v bodě je stejné na každé z nich. (Pokud by \(y\) ‚S byly jiné, tam by byl „skok“ v grafu!)

zkusme to pro funkce, které jsme použili výše:

Piecewise Function	Check Boundary Points
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\)	Let’s check \(x=4\) in both parts of the function, since 4 is the „boundary point”: \(\begin{array}{l}-2(4)+8=0\\\,\,\,\frac{1}{2}(4)-2=0\end{array}\) Od \(0=0\), tato funkce je po částech spojitá.
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\,\,\,\,\text{pokud }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{1 }\le x<4\\-5+x\,\,\,\,\,\,\,\,\,\text{pokud }x\ge 4\end{array} \right.\)	pojďme zkontrolovat první dvě části funkce. Poznámka v druhé části, \(y\) je vždy 2: \(\begin{array}{l}1+4=5\\\,\,\,\,\,\,\,\,\,2=2\end{array}\) Od \(5\ne 2\), můžeme zastavit tady, a všimněte si, že tato funkce je po částech non-kontinuální. Pokud by \(y\) ‚ S byly stejné, museli bychom jít jeden zkontrolovat další hraniční bod na \(x=4\).

Získání Rovnic z Funkce po Částech Grafů

můžete být požádáni, aby napsali po částech funkce, uveden graf. Nyní, když víme, o čem jsou jednotlivé funkce, není to tak špatné!

přezkoumat, jak získat rovnice z lineární grafy, viz Získání Rovnice přímky a z kvadratické rovnice, viz Hledání Kvadratická Rovnice z Bodů nebo Grafu.

zde jsou grafy s vysvětlením, jak odvodit jejich po částech rovnice:

Piecewise Function Graph	Procedure to get Function
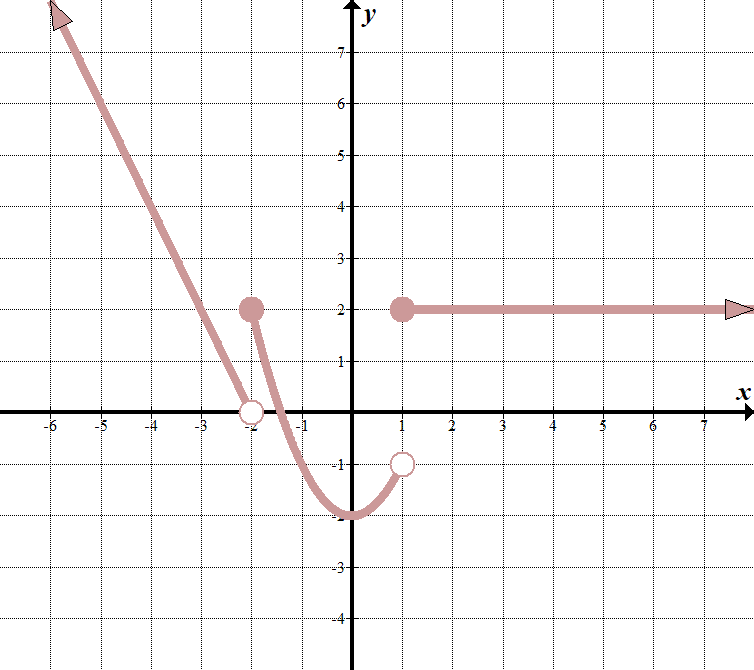	We see that our „boundary lines” are at \(x=-2\) and \(x=1\). We know that our function will look something like this (notice open and closed endpoints): \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\text{pokud }x<-2\\\text{ }……\,\,\,\,\,\,\,\,\text{pokud }-\text{2 }\le x<1\\\text{ }……\,\,\,\,\,\,\,\,\text{pokud }x\ge 1\end{array} \right.\) můžeme vybrat dva body \((-2,0)\) a \((-3,2)\) na nejlevější line získat rovnici \(y=-2x-4\). střední funkce je \(y={{x}^{2}}-2\), a funkce zcela vpravo je pouze vodorovná čára \(y=2\). funkce po částech je tedy: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x-4\,\,\,\,\,\,\,\text{pokud }x<-2\\\text{ }{{x,}^{2}}-2\,\,\,\,\,\,\,\,\,\,\text{pokud }-\text{2}\le x<1\\\text{ 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{pokud }x\ge 1\end{array} \right.\)
	vidíme, že naše „hranice“ je v \(x=5\). Protože se řádky setkávají na \((5,4)\), nezáleží na tom, kam umístíme znaménko \(\le \) nebo \(\ge \); prostě to nemůžeme dát na obě místa, jinak by to nebyla funkce. Máme tak daleko: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\,\text{pokud }x<5\\\text{ }……\,\,\,\,\,\,\,\,\,\text{pokud }x\ge 5\end{array} \right.\) opět se musíme podívat na každý řádek zvlášť, abychom určili jejich rovnice. Můžeme buď vzít 2 body z každého řádku, abychom je získali, nebo odvodit ze svahů a \(y\)–zachycení; funkce po částech je: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\frac{6}{5}x-2\,\,\,\,\,\,\,\text{pokud }x<5\\\frac{2}{5}x+2\,\,\,\,\,\,\,\text{pokud }x\ge 5\end{array} \right.\)

Absolutní Hodnota jako po Částech Funkce

můžeme psát absolutní hodnotu funkce jako po částech funkce – to je opravdu cool! Možná budete chtít zkontrolovat řešení rovnic a nerovností absolutní hodnoty, než budete pokračovat v tomto tématu.

řekněme, že máme funkci \(f\left (x \right)=\left / x\right|\). Z toho, co jsme se dozvěděli dříve, víme, že když je \(x\) kladné, protože bereme absolutní hodnotu, bude to stále jen \(x\). Ale když \(x\) je záporné, když vezmeme absolutní hodnotu, musíme vzít opak (negovat), protože absolutní hodnota musí být kladná. Dává to smysl? Takže například, kdybychom měli \(/5/\), vezmeme jen to, co je uvnitř absolutního znaménka, protože je to pozitivní. Ale pro \(|-5|\), musíme mít opačný (negativní), co je uvnitř absolutní hodnoty, aby to bylo \(\displaystyle 5\,\,\,(-\,-5=5)\).

to znamená, že tuto funkci absolutní hodnoty můžeme zapsat jako funkci po částech. Všimněte si, že můžeme získat „bod obratu“ nebo „hraniční bod“ nastavením toho, co je uvnitř absolutní hodnoty na 0. Pak můžeme buď použít původní funkci, nebo negovat funkci, v závislosti na znamení funkce (bez absolutní hodnoty) v daném intervalu.

například, můžeme napsat \(\displaystyle \left| x \right|\text{ }=\left\{ \begin{array}{l}x\,\,\,\,\,\,\,\,\,\text{pokud }x\ge 0\\-x\,\,\,\,\,\text{pokud }x<0\end{array} \right.\). Také si všimněte, že pokud je funkce spojitá (v hraničním bodě není žádný“ skok“), nezáleží na tom, kam umístíme znaky „menší nebo rovno“ (nebo „větší nebo rovno“), pokud je neopakujeme! Nemůžeme je opakovat, protože teoreticky nemůžeme mít dvě hodnoty \(y\) pro stejné \(x\), jinak bychom neměli funkci.

Here are more examples, with explanations. (You might want to review Quadratic Inequalities for the second example below):

Absolute Value Function	Method to get Piecewise Function
\(g\left( x \right)=\left| {2x+3} \right|\)	Let’s first find the „boundary line”. Děláme to tím, že nastavení, co je uvnitř absolutní hodnoty na 0, a pak řešení pro \(\boldsymbol{x}\). Když \(2x+3 \ ge 0\), dostaneme \(\displaystyle x\ge – \frac{3}{2}\) (ve skutečnosti můžeme zachovat \(\ge \), když řešíme). Když je \(2x+3\) kladné, bereme to „tak, jak je“, ale pokud je záporné, musíme celou věc negovat. proto je funkce po částech: \(\displaystyle \left| {2x+3} \right|=\left\{ \begin{array}{l}2x+3\,\,\,\,\,\,\,\,\,\text{pokud }x\ge\frac{3}{2}\text{ }\\-2x-3\,\,\,\,\,\text{pokud }x<-\frac{3}{2}\end{array} \right.\) zkuste to-funguje to!
\(f\left( x \right)=\left| {{{x}^{2}}-4} \right|\)	Pojďme nejdřív najít „boundary line(s)“; jsme si stanovili, co je uvnitř absolutní hodnoty na 0. Když \({{x}^{2}}-4 \ ge 0\), dostaneme \(x\le -2\) nebo \(x\ge 2\) (zkuste některá čísla!). Když je \({{x}^{2}}-4\) kladné, bereme to „tak, jak je“, ale pokud je záporné, musíme to negovat. po částech funkce je: \(\displaystyle \left| {{{x}^{2}}-4} \right|=\left\{ \begin{array}{l}{{x,}^{2}}-4\,\,\,\,\,\ text{pokud }x\le -2\\4-{{x,}^{2}}\,\,\,\,\,\text{pokud }-2<x<2\\{{x,}^{2}}-4\,\,\,\,\,\ text{pokud }x\ge 2\text{ }\end{array} \right.\) nebo \(\displaystyle \left| {{{x}^{2}}-4} \right|=\left\{ \begin{array}{l}{{x,}^{2}}-4\,\,\,\,\,\,\ text{pokud }x\le -2\text{ }\,\,\text{nebo}\,\,\text{ }x\ge 2\\4-{{x,}^{2}}\,\,\,\,\,\,\,\ text{pokud }-2<x<2\end{array} \right.\) Znovu (protože funkce je spojitá), je to opravdu nezáleží na tom, kde máme \(\le \) a \(\ge \) (na rozdíl od \(<\) a \(>\)), tak dlouho, jak jsme se je neopakovat.
\(f\left( x \right)=2x+\left| {x+2} \right|\)	Tohle je trochu složitější, protože máme \(x\) uvnitř a mimo absolutní hodnotu. Pro „hraniční čáru“ používáme pouze to, co je uvnitř absolutní hodnoty. Když \(x+2 \ ge 0\), dostaneme \(x\ge -2\). Ale pro funkci po částech musíme použít celou funkci, včetně části, která je mimo absolutní hodnotu. Funkce po částech je tedy: \(\displaystyle 2x+\left| {x+2} \right|=\left\{ \begin{array}{l}2x+x+2\,\,\,\,\,\text{pokud }x\ge -2\\2x-x-2\,\,\,\,\,\text{pokud }x<-2\end{array} \right.\) zkusme zjednodušit: \(\displaystyle 2x+\left| {x+2} \right|=\left\{ \begin{array}{l}3x+2\,\,\,\,\,\,\,\text{pokud }x\ge -2\\x-2\,\,\,\,\,\,\,\,\,\,\text{pokud }x<-2\end{array} \right.\) zkuste některé hodnoty menší než a skvělé pak -2; měly by fungovat!
\(g\left( x \right)=\left| {{{x}^{2}}-4x-5} \right|\)	Tohle je nejlepší řešit s nápisem grafu, protože máme kvadratické a potřebujeme vědět, kde je funkce kladná a záporná. nejprve faktor kvadratický uvnitř funkce absolutní hodnoty na \(\left ({x-5} \right)\left ({x+1} \right)\). Pak použijte znamení, grafu vidět, kde faktory jsou pozitivní a negativní, a pamatujte, že tam, kde faktory jsou pozitivní, můžeme použít funkci „jako je“, a tam, kde faktory jsou negativní, jsme negovat funkci: \(\displaystyle \left| {{{x}^{2}}-4x-5} \right|=\left\{ \begin{array}{l}{{x}^{2}}-4x-5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{pokud }x\le -1\,\,\,\,\text{nebo}\,\,\,\,x\ge 5\\-\left( {{{x}^{2}}-4x-5} \right)\,\,\,\,\text{pokud }-1<x<5\text{ }\end{array} \right.\)
\(\displaystyle g\left( x \right)=\frac{{\left| {x+2} \right|}}{{x+2}}\)	Toto je racionální funkce, protože tam je proměnná ve jmenovateli. Když \(x+2 \ ge 0\), dostaneme \(\displaystyle x \ ge -2\). Když \(x+2\) je pozitivní, jen jsme si to, „jak je“, ale pokud je to negativní, musíme negovat to, co je v absolutní hodnotě: \(\displaystyle \frac{{\left| {x+2} \right|}}{{x+2}}=\left\{ \begin{array}{l}\frac{{x+2}}{{x,+2}}\,\,\,\,\,\,\,\,\,\text{pokud }x\ge -2\\\frac{{-x-2}}{{x,+2}}\,\,\,\,\,\,\ text{pokud }x<-2\end{array} \right.\). Ale musíme být opatrní, protože \(x\ne 2\) (omezení domény: jmenovatel by byl 0). proto je funkce po částech: \(\displaystyle \frac{{\left| {x+2} \right|}}{{x+2}}=\left\{ \begin{array}{l}1\,\,\,\,\,\,\,\,\,\,\text{pokud }x>-2\\-1\,\,\,\,\,\,\text{pokud }x<-2\end{array} \right.\).

můžete také být vyzváni, aby absolutní hodnota, graf a napsat to jako po částech funkce:

Absolute Value Graph	Method to get Piecewise Function
	We see that our „boundary line” is at \(x=0\), so what’s inside the absolute value sign must be \(x\) or a factor of \(x\). (Je to proto, že abychom získali hraniční čáru s funkcí absolutní hodnoty, nastavíme to, co je uvnitř absolutní hodnoty, na 0, a vyřešíme pro \(x\)). Když \(x>0\), můžeme vidět, že rovnice přímky \(y=2x-2\). Když \(x<0\), rovnice je \(y=2x-2\). Můžeme zapsat toto jako po částech funkce: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}2x-2\,\,\,\,\,\,\,\text{pokud }x>0\\-2x-2\,\,\,\text{pokud }x\le 0\end{array} \right.\) můžeme to také napsat jako transformované absolutní hodnota funkce \(y=2\left| x \right|-2\) nebo \(y=\left| {2x} \right|-2\) (protože 2 je kladné, může být uvnitř nebo vně \(\left| {\,\,} \right|\)). (To dává smysl, protože, když to, co je uvnitř \(\left| {\,\,} \right|\) je \(> 0\), můžeme použít normální funkce \(y=2x-2\), a když to, co je uvnitř, je \(< 0\), jsme negovat absolutní hodnota, aby to \(y=-\left( {2x} \right)-2\)).
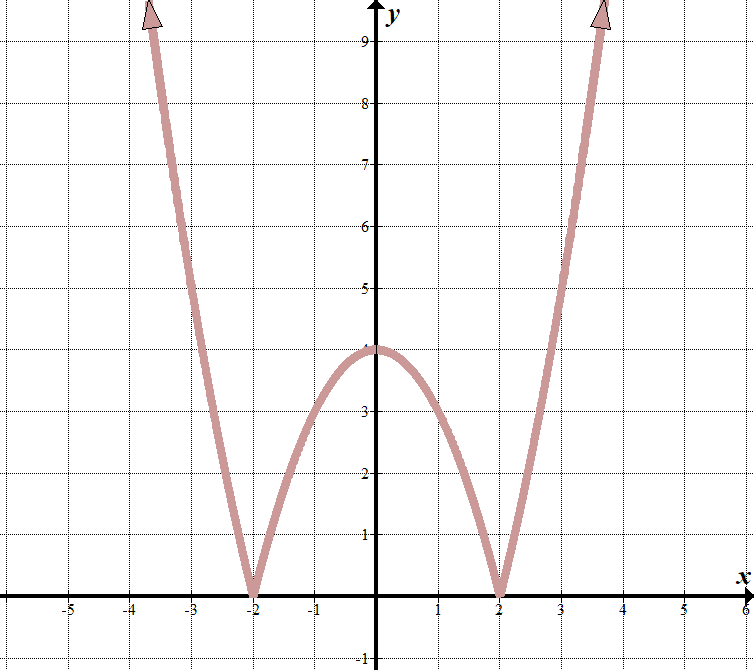	vidíme, že naše „hranice“ jsou \(x=2\) a \(x=-2\), takže to, co je uvnitř absolutní hodnoty musí mít faktory \(x-2\) a \(x+2\). Když \(x<-2\) nebo \(x>2\), můžeme vidět, že graf vypadá jako normální část grafu \(y={{x,}^{2}}-4\). (Přišel jsem na to tím, že jsem znal faktory a dobře odhadl!) Až \(-2<x<2\), rovnice je převrácený, nebo popřena (převrátil \(x\)-osa). Můžeme zapsat toto jako po částech funkce: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}{{x,}^{2}}-4\,\,\,\,\,\,\,\,\,\ text{pokud }x<-2\text{ nebo }x>2\\-{{x}^{2}}\text{+ 4}\,\,\,\,\,\,\text{pokud }-2\le x\le 2\end{array} \right.\) můžeme vidět, že to začalo transformované kvadratické funkce \(y={{x}^{2}}-4\) s absolutní hodnotou kolem něj, protože všechny \(y\) hodnoty jsou pozitivní: \(y=\left| {{{x}^{2}}-4} \right|\).
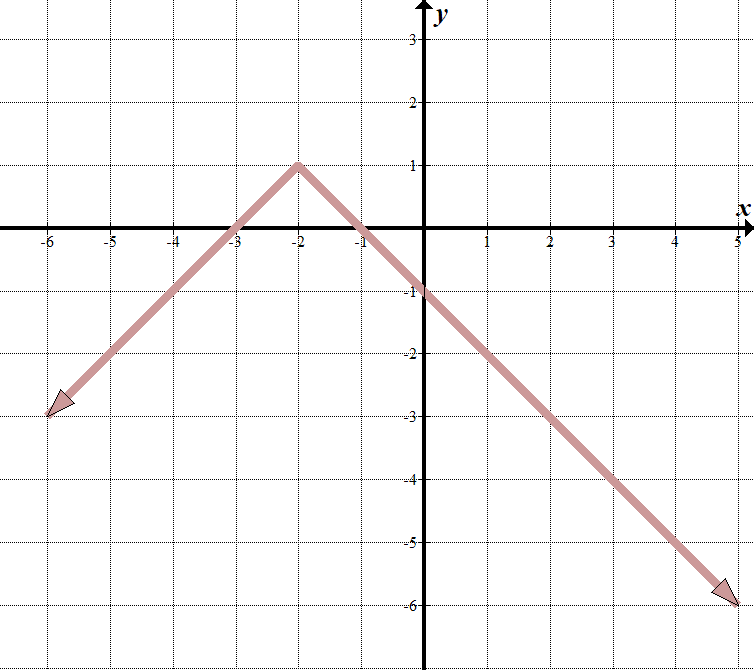	vidíme, že naše „hranice“ je v \(x=-2\), takže to, co je uvnitř absolutní hodnoty musí být \(x+2\). Když \(x>-2\), můžeme vidět, že rovnice řádku je \(y= – x-1\). Když \(x<-2\), řádek je \(y=x+3\). Můžeme zapsat toto jako po částech funkce: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-x-1\,\,\,\,\,\,\text{pokud }x>-2\\x+3\,\,\,\,\,\,\,\,\,\,\text{pokud }x\le -2\end{array} \right.\) je asi jednodušší to napsat jako transformovanou funkci absolutní hodnoty. Vidíme, že nadřazená funkce absolutní hodnoty je převrácena svisle, přesunout doleva 2, a nahoru 1. Naše rovnice absolutní hodnoty je \(y= – \left / {x+2} \right|\,\,+\,\,1\). To je stejné jako funkce po částech výše. Zkuste to-funguje to!

Transformace po Částech Funkce

Pojďme udělat transformaci po částech funkce. O rodičovských funkcích a jejich transformacích jsme se dozvěděli zde v sekci nadřazené Grafy a transformace. Pravděpodobně si budete chtít nejprve přečíst tuto sekci, než vyzkoušíte po částech transformaci.

Nechte je transformovat tyto funkce po částech otočil kolem \(x\)-ová osa svisle roztažen o faktor 2 jednotky, 1 jednotku a 3 jednotky.

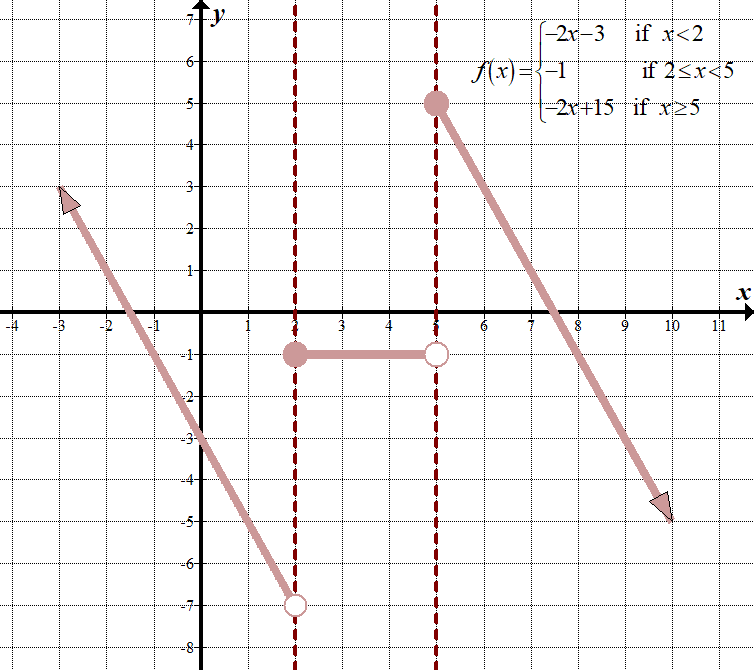
Budeme kreslit \(-2f\left( x-1 \right)+3\), kde:

\(\displaystyle f\left( x \right)=\left\{ \begin{align}x+4\,\,\,\,\,\,\,\,&\text{ pokud }x<&\text{ 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,&\text{ pokud }x\ge 4\end{align} \right.\)

ujistěte se, že používáme „hraniční“ body, když vyplníme T-graf pro transformaci. Nezapomeňte, že transformace uvnitř závorek se provádí na \(x\) (dělá opačnou matematiku) a venku se provádí na \(y\). Přijít s t-graf, jak je znázorněno v tabulce níže, můžeme použít klíčové body, včetně dvou bodů na každé „hraniční čáry“.

Všimněte si, že, protože tato transformace je složité, můžeme přijít s novou, po částech funkce přeměnou 3 „kousky“, a také transformace „\(x\)“s kde okrajové body jsou (přidáním 1 nebo vpravo 1), od té doby jsme se udělat pravý opak matematika pro „\(x\)“. Chcete-li získat nové funkce v každém intervalu, můžeme v původní rovnici nahradit „\(x-1\)“ za „\(x\)“, vynásobit -2 a poté přidat 3. Například, \(\displaystyle -2f\left( {x-1} \right)+3=-2\left+3=-2\left( {x+3} \right)+3=-2x-3\).

\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2\left( {\left( {x-1} \right)+4} \right)+3=-2x-3,\,\,\,\,\text{ pokud }x-1<1\,\,\,\left( {x<2} \right)\\-2\left( 2 \right)+3=-1,\,\,\,\,\text{ pokud }\,\text{ 2 }\le x<5\\-2\left( {\left( {x-1} \right)-5} \right)+3=-2x+15,\,\,\,\,\text{ pokud }x\ge 5\end{array} \right.\)

zde jsou grafy“ před „a“ po“, včetně T-grafu:

Piecewise Parent Function	T-chart	Transformation of Function
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\)	x + 1 x y –2y+3 1 0 4 –5 2 1 5 –7 2 1 2 –1 5 4 2 –1 5 4 –1 5 8 7 2 –1	\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2x-3\,\,\,\,\,\,\,\,\,\text{if }x<2\\-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 2}\le x<5\\-2x+15\,\,\,\,\,\,\text{if }x\ge 5\end{array} \right.\)

Piecewise Function Word Problems

Problem:

váš oblíbený pes groomer poplatky podle hmotnosti vašeho psa. Pokud je váš pes 15 liber a pod, groomer poplatky $ 35 . Pokud je váš pes mezi 15 a 40 liber, účtuje 40 dolarů. Pokud váš pes je u konce 40 liber, ona účtuje $ 40, plus další $ 2 za každou libru.

(a) napište po částech funkci, která popisuje, co váš pes groomer poplatky.

(b) graf funkce.

(c) co by se nabíjelo, kdyby váš roztomilý pes vážil 60 liber?

řešení:

(a) vidíme, že „hraniční body“ jsou 15 a 40, protože se jedná o váhy, kde se ceny mění. Protože máme dva hraniční body, budeme mít tři rovnice v naší funkci po částech. Musíme začít na 0, protože psi musí vážit 0 liber:

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\,\text{pokud }0<x\le 15\\\text{ }……\,\,\,\,\,\,\,\,\,\text{pokud }15<x\le 40\\\text{ }……\,\,\,\,\,\,\,\,\,\text{pokud }x>40\end{array} \right.\)

hledáme „odpovědi“ (kolik stojí péče) na „otázky“ (kolik váží pes) pro tři rozsahy cen. První dva jsou jen paušální poplatky (35$a 40$). Poslední rovnice je trochu složitější; groomer účtuje $ 40 plus $ 2 za každou libru nad 40. Zkusme reálná čísla: pokud váš pes váží 60 liber, bude účtovat 40 $plus 2 $\(20 (60-40)\). Změníme to na rovnici: \(40+2 (x–40)\), což zjednodušuje na \(2x-40\) (viz Jak 2 je sklon?).

celá funkce po částech je:

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{pokud }0<x\le 15\\\text{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{pokud }15<x\le 40\\\text{ }40+2\left( {x-40} \right)\,\,\,\,\,\,\text{pokud }x>40\end{array} \right.\) nebo \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{pokud }0<x\le 15\\\text{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{pokud }15<x\le 40\\\text{ }2x-40\,\,\,\,\,\,\,\text{pokud }x>40\end{array} \right.\)

(b) pojďme graf:Všimněte si, že tato rovnice po částech není spojitá. Také si uvědomte, že rozumná doména pro tento problém může být \(\left ({0,200} \right]\) (vzhledem k tomu, že psi neváží více než 200 liber!) a rozumný rozsah může být \(\left \ cup \left\).

(c) pokud váš pes váží 60 liber, můžeme použít graf nebo funkci, abychom zjistili,že budete muset zaplatit 80$. Whoa! To stojí víc než lidský účes(alespoň Moje účesy)!

problém:

plánujete prodat trička she Love Math jako sbírku. Velkoobchodní společnost t-shirt vám účtuje 10 dolarů za košili za prvních 75 košil. Po prvních 75 košilích, které si koupíte až 150 košil, společnost sníží cenu na 7,50 $za košili. Po zakoupení 150 košil se cena sníží na 5 $za košili. Napište funkci, která modeluje tuto situaci.

Řešení:

vidíme, že „hraniční body“ jsou 75 a 150, protože se jedná o počet triček koupil, kde ceny změnit. Protože máme dva hraniční body, budeme mít tři rovnice v naší funkci po částech. Začneme \(x\ge 1\), protože předpokládáme, že je zakoupena alespoň jedna košile. Poznámka: v tomto problému musí být počet zakoupených triček (\(x\)) nebo doména celé číslo, ale toto omezení by nemělo ovlivnit výsledek problému.

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\text{ pokud }1\le x\le 75\\\text{ }……\text{ pokud }75<x\le 150\\\text{ }……\text{ pokud }x>150\end{array} \right.\)

hledáme „odpovědi“ (celkové náklady na trička) na “ otázky „(kolik je zakoupeno) pro tři rozsahy cen.

pro až 75 košile, cena je $10, takže celková cena by \(10x\). U více než 75 košil, ale až 100 košil, je cena 7,50$, ale prvních 75 triček bude stále stát 10 $za košili. Druhá funkce zahrnuje $ 750 vynaložené na prvních 75 košile (75 krát $ 10), a také zahrnuje $ 7.50 násobek počtu košile nad 75, což by bylo \((x-75)\). Například, pokud jste si koupili 80 košile, budete muset strávit \(\$10\times 75=\$750\) a \(\$7.50\times 5\,\) (80 – 75) pro košile po 75 tričko.

podobně za více než 150 košil bychom stále platili cenu $ 10 až 75 košil, $7.50 cena za 76 na 150 košile (75 více košile), a pak $ 5 za košili za počet košile koupil přes 150. Zaplatíme \(10(75)+7.50(75)+5(x-150)\) Pro \(x\) košile. Vložte čísla a zkuste to!

, celé po částech funkce je:

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{pokud }1\le x\le 75\\\text{ }7,5 x\text{ }+\text{ }187.5\,\,\,\,\,\text{7}5<x\le 150\\\text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\text{ if }x> 150 \ end{array} \right.\) nebo \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{pokud }1\le x\le 75\\\text{ }7,5 x\text{ }+\text{ }187.5\,\,\,\,\,\text{7}5<x\le 150\\\text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\,\text{pokud }x>150\end{array} \right.\)

problém:

autobusová doprava stojí 50 $za prvních 400 mil a každá další 300 mil (nebo jejich zlomek) přidá 10 $k jízdnému.

použijte funkci po částech k reprezentaci jízdného autobusu z hlediska vzdálenosti v mílích.

Řešení:

Toto je ve skutečnosti složitější problém, ale pojďme nejprve přemýšlet jako první o „hraniční bod“, což je 400. Je to docela jednoduché, když je jízda menší než 400 mil; cena je $ 50 .

pro více než 400 mil musíme odečíst prvních 400 mil (ale nezapomeňte zahrnout prvních 50$), vydělit počet mil zbývajících 300 mil (a zaokrouhlit nahoru, pokud existuje zlomková částka)a vynásobit to 10$.

ošemetná část je, když „zaokrouhlujeme“ na část příštích 300 mil. Můžeme použít „strop“ funkce (určené volbou \(\left\lceil {} \right\rceil \)); tato funkce dává nejmenší celé číslo, které je větší než nebo rovnající se jeho vstup; například, strop 3,5 a 4 je 4.

to je to, co máme:

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }50\text{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{pokud }0\le x\le 400\\\text{ }50+10\times \left\lceil {\frac{{x,-400}}{{300}}} \ právo\rceil \text{ }\,\,\,\,\,\,\text{ pokud }x>400\end{array} \right.\)

zkusme to! Pokud máme 1500 kilometrů jízdy, náklady by \(\displaystyle 50+10\times \left\lceil {\frac{{1500-400}}{{300}}} \právo\rceil \text{ }=50+10\times 4=\$90\).

problém:

jaká hodnota \(\boldsymbol{a}\) by tuto funkci po částech spojila?

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}3{{x,}^{2}}+4\,\,\,\,\,\ text{ pokud }x<-2\\5x+\boldsymbol{o}\,\,\,\,\,\,\,\,\text{pokud }x\ge -2\end{array} \right.\)

Řešení:

Pro po částech funkce musí být spojitá, na hranici bod (bod, kde se funkce mění), \(y\) hodnoty musí být stejné. Můžeme připojit -2 pro \(x\) v obou funkcí a ujistěte se, že \(y\) jsou stejné

\(\begin{align}3{{x}^{2}}+4&=5x+\\3{{\left( {-2} \right)}^{2}}+4&=5\left( {-2} \right)+\\12+4&&=26\end{align}\)

Pokud \(a=26\), po částech funkce je spojitá!

Naučte se tato pravidla a cvičte, cvičte, cvičte!

více praxe: použijte Mathway widget níže, aby se pokusili napsat po částech funkci. Klikněte na Odeslat (modrá šipka napravo od problému) a klikněte na napsat absolutní hodnotu po částech, abyste viděli odpověď.

můžete také zadat svůj vlastní problém, nebo klikněte na tři tečky v pravém horním rohu a klikněte na „Příklady“ drill-down podle tématu.

Pokud jste klepněte na Klepněte na pro zobrazení kroky, nebo Klikněte Zde, můžete se zaregistrovat na Mathway pro bezplatné zkušební verze, a potom inovovat na placené předplatné kdykoliv (aby se jakýkoli typ matematický problém vyřešen!).

na matice a řešení systémů s maticemi – jste připraveni!