Konigsberg je město na řece Preger, které bylo v 18.století německým městem, ale nyní je ruské. Ve městě jsou dva ostrovy, které jsou spojeny s břehy sedmi mosty (jak je znázorněno níže).

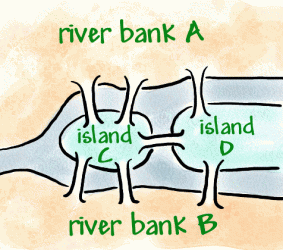
To se stalo tradicí, aby se pokusili projít po městě způsobem, thatonly přešel každý most jednou, ale to se ukázalo být difficultproblem. Leonhard Euler, švýcarský matematik ve služběruská císařovna Kateřina Veliká, slyšela o problému.V roce 1736 Euler dokázal, že procházka nebyla možná. Dokázal to tím, že vynalezl druh diagramu zvaného síťje tvořen vrcholy(tečky, kde se setkávají čáry) a oblouky (čáry).

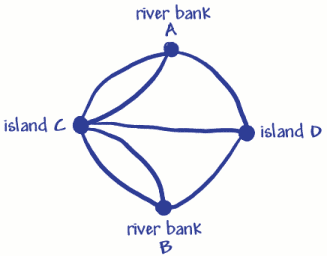
použil čtyři body (vrcholy) pro dva břehy a twoislands. Ty byly označeny A, B A C, D. sedm řádků (oblouků) je sedm mostů. Můžete vidět, že 3 mosty (oblouky)se připojí k břehu řeky A a 3 se připojí k břehu řeky B. 5 mostů (oblouků)se připojí k ostrovu C a 3 se připojí k ostrovu D. To znamená, že vševertice mají lichý počet oblouků, takže se nazývají oddvertice. (Sudý vrchol by musel mít sudý počet oblouků).
Nezapomeňte, že problém byl cestovat po městě přes každý most jen jednou. V eulerově síti to znamenalo sledovat každý z nich pouze jednou a navštívit všechny vrcholy. Euler dokázal, že to nemůže být provedeno, protože zjistil, že chcete-li mít lichý vrchol, musíte začít nebo ukončit výlet na tomto vrcholu. (Přemýšlejte o tom).Protože může existovat pouze jeden začátek a jeden konec, mohou existovat pouze dva liché vrcholy, pokud budete moci sledovat každý Arc pouze jednou. Vzhledem k tomu, most problém má 4 liché vrcholy, to justisn ‚ t možné udělat! Co se stane, pokud nejsou vůbec žádné liché vrcholy? Lze tuto síť vysledovat?

vynález sítí začal zcela nový typ geometrie calledTopology. Topologie se nyní používá mnoha způsoby, včetně plánovánía mapování železničních sítí. (Ahhh! Vlaky do ní musely přijet….)