Toto je čekající revize této stránky. Může se lišit od poslední přijaté revize, která byla přijata dne 13. ledna 2011.

molární objem (Vm symbol) látky je objem, který zaujímá jeden mol látky při dané teplotě a tlaku. To se rovná molekulové hmotnosti (M) látek rozdělených podle jeho hustoty (ρ) při dané teplotě a tlaku:

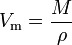
To má jednotky z metrů krychlových na mol (m3/mol). Nicméně, molární objemy jsou často vyjádřeny jako kubických metrů za 1000 molů (m3/kmol) nebo krychlové na mol (dm3/mol) pro plyny a jak centimetrů na mol (cm3/mol) pro kapaliny a pevné látky.

je-li látka směsí obsahující n složek, vypočte se molární objem pomocí:

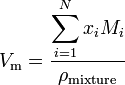
kde x i je molární zlomek i-té složky, M je molekulová hmotnost i-té složky a pmixture je hustota směsi při dané teplotě a tlaku.

při zadávání číselných hodnot molárního objemu je důležité také uvést dané podmínky teploty a tlaku. V opačném případě jsou číselné hodnoty bezvýznamné.

Ideální plyny

ideálního plynu rovnice lze upravit, aby tento výraz pro molární objem ideálního plynu:

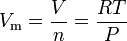
Kde v jednotkách SI:

= plynu absolutní tlak v Pa,

= počet molů v mol

= plyn, molární objem, v m3/mol

= plynu absolutní teplota v K,

= univerzální plynová konstanta z 8.314472 m3·Pa·mol-1·K-1

Kde v USA obvyklé jednotky:

= plynu absolutní tlak v psia

= počet molů, v lb-mol

= plyn, molární objem, v ft3/lb-mol

= plynu absolutní teplota ve stupních Rankina (°R),

= univerzální plynová konstanta z 10.7316 ft3·psia·lb-mol-l·°R-1

Příklad výpočtů pro ideální plyn, molární objemy:

• V SI metrické jednotky:

Pj = 8.314472 × 273.15 / 101,325 = 0.022414 m3/mol při teplotě 0 °C a 101,325 Pa absolutní tlak = 22.414 m3/kmol při 0 °C (273.15 K) a 101.325 kPa absolutní tlak Vm = 8.314472 × 273.15 / 100,000 = 0.022711 m3/kmol při 0 °C a 100 000 Pa absolutní tlak = 22.711 m3/kmol při 0 °C (273.15 K) a 100 kPa absolutní tlak

• V USA zvykem jednotky:

Pj = 10.7316 × 519.67 / 14.696 = 379.48 ft3/lb-mol při teplotě 60 °F (519.67 °R) a 14.696 psia

Poznámky:

• lb-mol je zkratka pro pound-mol
• °R je stupňů Rankina (absolutní teplotní stupnice) a °F stupně Celsia (teplotní stupnice).
• °R = °F + 459.67
• technická literatura může být matoucí, protože někteří autoři se často nedaří vysvětlit, zda jsou pomocí univerzální plynová konstanta R, které se vztahuje na jakýkoliv ideální plyn, nebo zda jsou pomocí specifických plynová konstanta R, které se vztahuje pouze na konkrétní plyn. Vztah mezi těmito dvěma konstantami je Rs = R / M, kde M je molekulová hmotnost plynu.

reálné plyny

reálné plyny jsou plyny, které nevykazují ideální chování plynů. Pro tyto plyny, nejjednodušší způsob stanovení molární objem je pomocí stlačitelnosti faktory, jako v následující výraz:

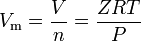
kde Z je plyn stlačitelnost faktor, což je užitečné termodynamická vlastnost pro změnu ideálního plynu na účet pro chování reálných plynů. Výše uvedená rovnice je v podstatě jednoduchá rovnice stavu (EOS). Hlavní omezení této rovnice stavu je, že plyn stlačitelnost faktor, Z, není konstantní, ale mění se z jednoho plynu do druhého, stejně jako teplota a tlak plynu v úvahu.

přesnější hodnoty reálného plynu molární objemy mohou být získané pomocí rovnic státu, jako jsou van der Waalsovy rovnice vyvinuté v roce 1873, Redlich-Kwong rovnice vyvinut v roce 1949, Soave-Redlich-Kwong rovnice vyvinut v roce 1972 a Peng-Robinson rovnice vyvinutý v roce 1976.

Nějaký obsah na této stránce mohou dříve objevily na Citizendium.