některé zajímavé věci o úhlech a kruzích.
- Vepsaný Úhel,
- Vepsaný Úhel, Věty
- příklad: jaká je velikost úhlu POQ? (O je circle center)
- Příklad: Jaká je velikost Úhlu CBX?
- Úhel v Půlkruhu (thaletova Věta)
- Další Dobrý Důvod, Proč To Funguje
- příklad: jaká je velikost úhlu BAC?
- Nalezení Kružnice je Střed
- Tětivový Čtyřúhelník
- Příklad: Jaká je velikost Úhlu WXY?
Vepsaný Úhel,
za Prvé, definice:
Vepsaný Úhel: úhel vyrobeny z bodů sedí na obvodu kruhu.
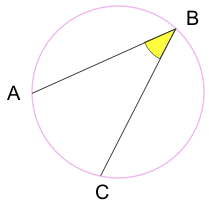
a a C jsou „koncové body“
B je „apex bod“
Hrát si s ním tady:
Při přesunu bodu „B“, co se stane s úhlem?
Vepsaný Úhel, Věty
vepsaný úhel a° je polovina středový úhel 2a°
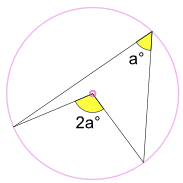
(Nazývá Úhel v Centru Věta)
A (udržování koncových bodů pevné) …
… úhel a° je vždy stejný,
bez ohledu na to, kde je na stejném oblouku mezi koncové body:
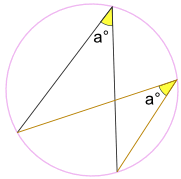
Úhel° je stejný.
(nazývané úhly Subtended stejným obloukovým Teorémem)
příklad: jaká je velikost úhlu POQ? (O je circle center)
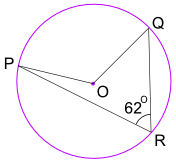
Úhlu POQ = 2 × Úhel PRQ = 2 × 62° = 124°
Příklad: Jaká je velikost Úhlu CBX?
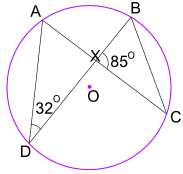
Úhel ADB = 32° také rovná Úhlu ACB.
A úhel ACB se také rovná úhlu XCB.
takže v trojúhelníku BXC známe úhel BXC = 85° A úhel XCB = 32°
Nyní použijte úhly trojúhelníku přidat na 180° :
Úhel v Půlkruhu (thaletova Věta)
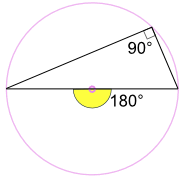
úhel vepsaný po obvodu kruhu a jeho průměru je vždy pravý úhel.:
(koncové body jsou buď konec kruhu je průměr,
apex bod může být kdekoliv na obvodu.)
|
proč? Protože: vepsaný úhel 90° je polovina středový úhel 180° (Pomocí „Úhel na Centrum Věta“ výše) |
 |
Další Dobrý Důvod, Proč To Funguje
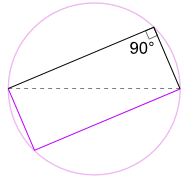
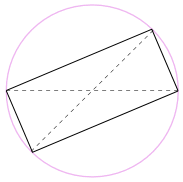
také Jsme to mohli otočit tvar o 180°, aby obdélník!
je to obdélník, protože všechny strany jsou rovnoběžné a obě úhlopříčky jsou stejné.
a tak jeho vnitřní úhly jsou všechny pravé úhly (90°).
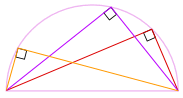
tak jdeme na to! Bez ohledu na to, kde je tento úhel
na obvodu, je vždy 90°
příklad: jaká je velikost úhlu BAC?
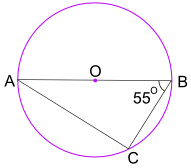
Úhel v Půlkruhu Věta nám říká, že Úhel ACB = 90°,
Nyní použijte úhlů v trojúhelníku je 180°, aby najít Úhel BAC:
Nalezení Kružnice je Střed
můžeme použít tuto myšlenku najít circle center:
- nakreslit pravý úhel z libovolného místa na obvodu kruhu, a pak kreslit průměr, kde dvě nohy narazí na kruh
- udělat znovu, ale na jiný průměr
Kde průměry kříž je centrem!
Tětivový Čtyřúhelník
|
„Cyklické“ Čtyřúhelník má všechny vrcholy na obvodu kruhu: |
 |
|
Tětivový Čtyřúhelník je opačné úhly přidat až 180°:
|
 |
Příklad: Jaká je velikost Úhlu WXY?
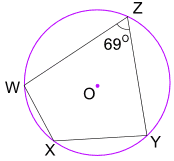
Opposite angles of a cyclic quadrilateral add to 180°

